The Gravitational Force
A gravitational force 
on a body is a certain type of pull that is directed toward a second body. In these early chapters, we do not discuss the nature of this force and usually consider situations in which the second body is Earth. Thus, when we speak of the gravitational force on a body, we usually mean a force that pulls on it directly toward the center of Earth—that is, directly down toward the ground. We shall assume that the ground is an inertial frame.
Suppose a body of mass m is in free fall with the free-fall acceleration of magnitude g. Then, if we neglect the effects of the air, the only force acting on the body is the gravitational force . We can relate this downward force and downward acceleration with Newton’s second law 
. We place a vertical y axis along the body’s path, with the positive direction upward. For this axis, Newton’s second law can be written in the form Fnet,y = may, which, in our situation, becomes
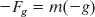
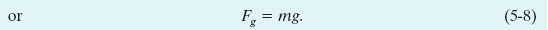
In words, the magnitude of the gravitational force is equal to the product mg.
This same gravitational force, with the same magnitude, still acts on the body even when the body is not in free fall but is, say, at rest on a pool table or moving across the table. (For the gravitational force to disappear, Earth would have to disappear.)
We can write Newton’s second law for the gravitational force in these vector forms:
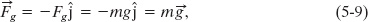
where 
is the unit vector that points upward along a y axis, directly away from the ground, and 
is the free-fall acceleration (written as a vector), directed downward.
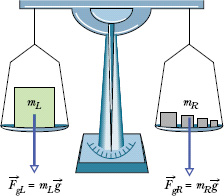
Fig. 5-6 An equal-arm balance. When the device is in balance, the gravitational force 
on the body being weighed (on the left pan) and the total gravitational force 
on the reference bodies (on the right pan) are equal. Thus, the mass mL of the body being weighed is equal to the total mass mR of the reference bodies.
Weight
The weight W of a body is the magnitude of the net force required to prevent the body from falling freely, as measured by someone on the ground. For example, to keep a ball at rest in your hand while you stand on the ground, you must provide an upward force to balance the gravitational force on the ball from Earth. Suppose the magnitude of the gravitational force is 2.0 N. Then the magnitude of your upward force must be 2.0 N, and thus the weight W of the ball is 2.0 N. We also say that the ball weighs 2.0 N and speak about the ball weighing 2.0 N.
A ball with a weight of 3.0 N would require a greater force from you—namely, a 3.0 N force—to keep it at rest. The reason is that the gravitational force you must balance has a greater magnitude—namely, 3.0 N. We say that this second ball is heavier than the first ball.
Now let us generalize the situation. Consider a body that has an acceleration 
of zero relative to the ground, which we again assume to be an inertial frame. Two forces act on the body: a downward gravitational force and a balancing upward force of magnitude W. We can write Newton’s second law for a vertical y axis, with the positive direction upward, as
In our situation, this becomes
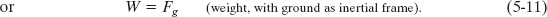
This equation tells us (assuming the ground is an inertial frame) that
The weight W of a body is equal to the magnitude Fg of the gravitational force on the body.
Substituting mg for Fg from Eq. 5-8, we find
which relates a body’s weight to its mass.
To weigh a body means to measure its weight. One way to do this is to place the body on one of the pans of an equal-arm balance (Fig. 5-6) and then place reference bodies (whose masses are known) on the other pan until we strike a balance (so that the gravitational forces on the two sides match). The masses on the pans then match, and we know the mass of the body. If we know the value of g for the location of the balance, we can also find the weight of the body with Eq. 5-12.
We can also weigh a body with a spring scale (Fig. 5-7). The body stretches a spring, moving a pointer along a scale that has been calibrated and marked in either mass or weight units. (Most bathroom scales in the United States work this way and are marked in the force unit pounds.) If the scale is marked in mass units, it is accurate only where the value of g is the same as where the scale was calibrated.
The weight of a body must be measured when the body is not accelerating vertically relative to the ground. For example, you can measure your weight on a scale in your bathroom or on a fast train. However, if you repeat the measurement with the scale in an accelerating elevator, the reading differs from your weight because of the acceleration. Such a measurement is called an apparent weight.
Caution: A body’s weight is not its mass. Weight is the magnitude of a force and is related to mass by Eq. 5-12. If you move a body to a point where the value of g is different, the body’s mass (an intrinsic property) is not different but the weight is. For example, the weight of a bowling ball having a mass of 7.2 kg is 71 N on Earth but only 12 N on the Moon. The mass is the same on Earth and Moon, but the free-fall acceleration on the Moon is only 1.7 m/s2.
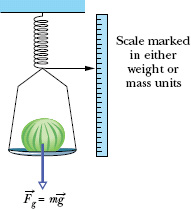
Fig. 5-7 A spring scale. The reading is proportional to the weight of the object on the pan, and the scale gives that weight if marked in weight units. If, instead, it is marked in mass units, the reading is the object’s weight only if the value of g at the location where the scale is being used is the same as the value of g at the location where the scale was calibrated.
The Normal Force
If you stand on a mattress, Earth pulls you downward, but you remain stationary. The reason is that the mattress, because it deforms downward due to you, pushes up on you. Similarly, if you stand on a floor, it deforms (it is compressed, bent, or buckled ever so slightly) and pushes up on you. Even a seemingly rigid concrete floor does this (if it is not sitting directly on the ground, enough people on the floor could break it).
The push on you from the mattress or floor is a normal force 
. The name comes from the mathematical term normal, meaning perpendicular: The force on you from, say, the floor is perpendicular to the floor.
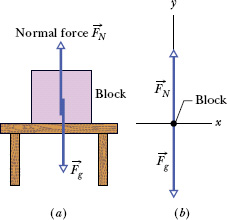
Fig. 5-8 (a) A block resting on a table experiences a normal force perpendicular to the tabletop. (b) The free-body diagram for the block.
When a body presses against a surface, the surface (even a seemingly rigid one) deforms and pushes on the body with a normal force 
that is perpendicular to the surface.
Figure 5-8a shows an example. A block of mass m presses down on a table, deforming it somewhat because of the gravitational force on the block. The table pushes up on the block with normal force . The free-body diagram for the block is given in Fig. 5-8b. Forces and are the only two forces on the block and they are both vertical. Thus, for the block we can write Newton’s second law for a positive-upward y axis (Fnet,y = may) as
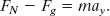
From Eq. 5-8, we substitute mg for Fg, finding
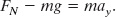
Then the magnitude of the normal force is
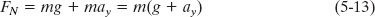
for any vertical acceleration ay of the table and block (they might be in an accelerating elevator). If the table and block are not accelerating relative to the ground, then ay = 0 and Eq. 5-13 yields
CHECK POINT 4 In Fig. 5-8, is the magnitude of the normal force 
greater than, less than, or equal to mg if the block and table are in an elevator moving upward (a) at constant speed and (b) at increasing speed?
Friction
If we either slide or attempt to slide a body over a surface, the motion is resisted by a bonding between the body and the surface. (We discuss this bonding more in the next chapter.) The resistance is considered to be a single force 
, called either the frictional force or simply friction. This force is directed along the surface, opposite the direction of the intended motion (Fig. 5-9). Sometimes, to simplify a situation, friction is assumed to be negligible (the surface is frictionless).
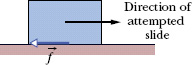
Fig. 5-9 A frictional force opposes the attempted slide of a body over a surface.
Tension
When a cord (or a rope, cable, or other such object) is attached to a body and pulled taut, the cord pulls on the body with a force 
directed away from the body and along the cord (Fig. 5-10a). The force is often called a tension force because the cord is said to be in a state of tension (or to be under tension), which means that it is being pulled taut. The tension in the cord is the magnitude T of the force on the body. For example, if the force on the body from the cord has magnitude T = 50 N, the tension in the cord is 50 N.
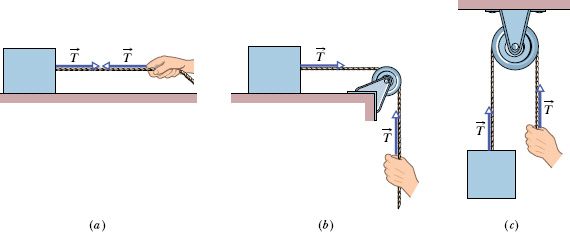
Fig. 5-10 (a) The cord, pulled taut, is under tension. If its mass is negligible, the cord pulls on the body and the hand with force , even if the cord runs around a massless, frictionless pulley as in (b) and (c).
A cord is often said to be massless (meaning its mass is negligible compared to the body’s mass) and unstretchable. The cord then exists only as a connection between two bodies. It pulls on both bodies with the same force magnitude T, even if the bodies and the cord are accelerating and even if the cord runs around a massless, frictionless pulley (Figs. 5-10b and c). Such a pulley has negligible mass compared to the bodies and negligible friction on its axle opposing its rotation. If the cord wraps halfway around a pulley, as in Fig. 5-10c, the net force on the pulley from the cord has the magnitude 2T.
CHECK POINT 5 The suspended body in Fig. 5-10c weighs 75 N. Is T equal to, greater than, or less than 75 N when the body is moving upward (a) at constant speed, (b) at increasing speed, and (c) at decreasing speed?
PROBLEM – SOLVING TACTICS
TACTIC 6 : Normal Force
Equation 5-14 for the normal force on a body holds only when is directed upward and the body’s vertical acceleration is zero; so we do not apply it for other orientations of or when the vertical acceleration is not zero. Instead, we must derive a new expression for from Newton’s second law.
We are free to move around in a figure as long as we maintain its orientation. For example, in Fig. 5-8a we can slide it downward so that its head is at the boundary between block and tabletop. However, is least likely to be misinterpreted when its tail is either at that boundary or somewhere within the block (as shown). An even better technique is to draw a free-body diagram as in Fig. 5-8b, with the tail of directly on the dot or sketch representing the block.
Takeoff illusion. Your sense of vertical depends on visual clues and on the vestibular system located in your inner ear. That system contains tiny hair cells in a fluid. When you hold your head upright, the hairs are vertically in line with the gravitational force on you and the system signals your brain that your head is upright. When you tilt your head backward by some angle 
, the hairs are bent and the system signals your brain about the tilt. The hairs are also bent when you are accelerated forward by an applied horizontal force 
. The signal sent to your brain then indicates, erroneously, that your head is tilted back, to be in line with an extension through the vector sum 
(Fig. 5-11a). However, the erroneous signal is ignored when visual clues clearly indicate no tilt, such as when you are accelerated in a car.
A pilot being hurled along the deck of an aircraft carrier at night has almost no visual clues. The illusion of tilt is strong and very convincing, with the result that the pilot feels as though the plane leaves the deck headed sharply upward. Without proper training, a pilot will attempt to level the plane by bringing its nose sharply down, sending the plane into the ocean.
Suppose that, starting from rest, a pilot undergoes constant horizontal acceleration to reach a takeoff speed of 85 m/s in 90 m. What is the angle of the illusionary tilt experienced by the pilot?
Solution: We need to find the tilt angle of the line that extends through 
, the vector sum of the vertical gravitational force acting on the pilot and the horizontal force applied to the pilot by the seatback. Our first Key Idea is that we can find by rearranging the force vectors as in Fig. 5-11b and then writing
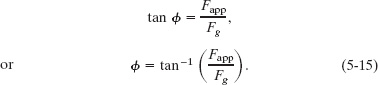
Our second Key Idea is that we can use Newton’s second law to relate the magnitude Fapp of the applied force to the pilot’s acceleration ax: Fapp = max, where m is the mass of the pilot. The third Key Idea is that because the acceleration is constant, we can use the equations of Table 2-1 to find ax. Since we know the initial speed (v0 = 0), the final speed (vx = 85 m/s), and the displacement (x − x0 = 90 m), we use Eq. 2-16 
to write
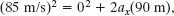
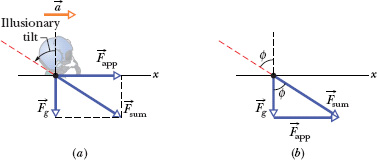
Fig. 5-11 (a) Force , directed to the right, is applied to the pilot during takeoff. The pilot’s head feels as though it is tilted back along the red dashed line. (b) The vector sum 
is at angle from the vertical.
Then, by Newton’s second law, Fapp = m(40.1 m/s2). Substituting this result and the result Fg = m(9.8 m/s2) in Eq. 5-15 gives us
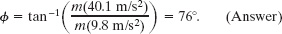
Thus, as the plane is accelerated along the carrier deck, the pilot feels an illusion of a backward tilt of 76°, as though the plane is angled nose-up by 76°. The illusion may compel the pilot to put the plane nose-down by 76° just after takeoff.
5-8 Newton’s Third Law
Two bodies are said to interact when they push or pull on each other—that is, when a force acts on each body due to the other body. For example, suppose you position a book B so it leans against a crate C (Fig. 5-12a). Then the book and crate interact: There is a horizontal force 
on the book from the crate (or due to the crate) and a horizontal force 
on the crate from the book (or due to the book). This pair of forces is shown in Fig. 5-12b. Newton’s third law states that
Newton’s Third Law: When two bodies interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction.
For the book and crate, we can write this law as the scalar relation
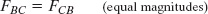
or as the vector relation
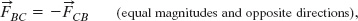
where the minus sign means that these two forces are in opposite directions. We can call the forces between two interacting bodies a third-law force pair. When any two bodies interact in any situation, a third-law force pair is present. The book and crate in Fig. 5-12a are stationary, but the third law would still hold if they were moving and even if they were accelerating.
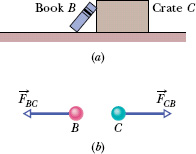
Fig. 5-12 (a) Book B leans against crate C. (b) Forces (the force on the book from the crate) and (the force on the crate from the book) have the same magnitude and are opposite in direction.
As another example, let us find the third-law force pairs involving the cantaloupe in Fig. 5-13a, which lies on a table that stands on Earth. The cantaloupe interacts with the table and with Earth (this time, there are three bodies whose interactions we must sort out).
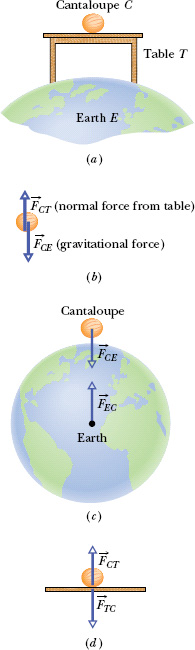
Fig. 5-13 (a) A cantaloupe lies on a table that stands on Earth. (b) The forces on the cantaloupe are 
and 
. (c) The third-law force pair for the cantaloupe–Earth interaction. (d) The third-law force pair for the cantaloupe–table interaction.
Let’s first focus on the forces acting on the cantaloupe (Fig. 5-13b). Force is the normal force on the cantaloupe from the table, and force is the gravitational force on the cantaloupe due to Earth. Are they a third-law force pair? No, because they are forces on a single body, the cantaloupe, and not on two interacting bodies.
To find a third-law pair, we must focus not on the cantaloupe but on the interaction between the cantaloupe and one other body. In the cantaloupe–Earth interaction (Fig. 5-13c), Earth pulls on the cantaloupe with a gravitational force and the cantaloupe pulls on Earth with a gravitational force 
. Are these forces a third-law force pair? Yes, because they are forces on two interacting bodies, the force on each due to the other. Thus, by Newton’s third law,
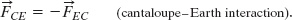
Next, in the cantaloupe–table interaction, the force on the cantaloupe from the table is and, conversely, the force on the table from the cantaloupe is 
(Fig. 5-13d). These forces are also a third-law force pair, and so
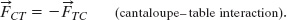
CHECK POINT 6 Suppose that the cantaloupe and table of Fig. 5-13 are in an elevator cab that begins to accelerate upward. (a) Do the magnitudes of 
and 
increase, decrease, or stay the same? (b) Are those two forces still equal in magnitude and opposite in direction? (c) Do the magnitudes of 
and 
increase, decrease, or stay the same? (d) Are those two forces still equal in magnitude and opposite in direction?
Leave a Reply