In pure translation, motion with a constant linear acceleration (for example, that of a falling body) is an important special case. In Table 2-1, we displayed a series of equations that hold for such motion.
In pure rotation, the case of constant angular acceleration is also important, and a parallel set of equations holds for this case also. We shall not derive them here, but simply write them from the corresponding linear equations, substituting equivalent angular quantities for the linear ones. This is done in Table 10-1, which lists both sets of equations (Eqs. 2-11 and 2-15 to 2-18; 10-12 to 10-16).
Recall that Eqs. 2-11 and 2-15 are basic equations for constant linear acceleration—the other equations in the Linear list can be derived from them. Similarly, Eqs. 10-12 and 10-13 are the basic equations for constant angular acceleration, and the other equations in the Angular list can be derived from them. To solve a simple problem involving constant angular acceleration, you can usually use an equation from the Angular list (if you have the list). Choose an equation for which the only unknown variable will be the variable requested in the problem. A better plan is to remember only Eqs. 10-12 and 10-13, and then solve them as simultaneous equations whenever needed. An example is given in Sample Problem 10-3.
![]() CHECK POINT 2 In four situations, a rotating body has angular position θ(t) given by (a) θ = 3t − 4, (b) θ = −5t3 + 4t2 + 6, (c) θ = 2/t2 − 4/t, and (d) θ = 5t2 − 3. To which situations do the angular equations of Table 10-1 apply?
CHECK POINT 2 In four situations, a rotating body has angular position θ(t) given by (a) θ = 3t − 4, (b) θ = −5t3 + 4t2 + 6, (c) θ = 2/t2 − 4/t, and (d) θ = 5t2 − 3. To which situations do the angular equations of Table 10-1 apply?
A grindstone (Fig. 10-8) rotates at constant angular acceleration α = 0.35 rad/s2. At time t = 0, it has an angular velocity of ω0 = −4.6 rad/s and a reference line on it is horizontal, at the angular position θ0 = 0.
(a) At what time after t = 0 is the reference line at the angular position θ = 5.0 rev?
Solution: The Key Idea here is that the angular acceleration is constant, so we can use the rotation equations of Table 10-1. We choose Eq. 10-13,
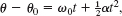
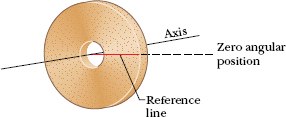
Fig. 10-8 A grindstone. At t = 0 the reference line (which we imagine to be marked on the stone) is horizontal.
because the only unknown variable it contains is the desired time t. Substituting known values and setting θ0 = 0 and θ = 5.0 rev = 10π rad give us
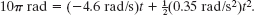
(We converted 5.0 rev to 10π rad to keep the units consistent.) Solving this quadratic equation for t, we find

(b) Describe the grindstone’s rotation between t = 0 and t = 32 s.
Solution: The wheel is initially rotating in the negative (clockwise) direction with angular velocity ω0 = −4.6 rad/s, but its angular acceleration α is positive. This initial opposition of the signs of angular velocity and angular acceleration means that the wheel slows in its rotation in the negative direction, stops, and then reverses to rotate in the positive direction. After the reference line comes back through its initial orientation of θ = 0, the wheel turns an additional 5.0 rev by time t = 32 s.
(c) At what time t does the grindstone momentarily stop?
Solution: We again go to the table of equations for constant angular acceleration, and again we need an equation that contains only the desired unknown variable t. However, now we use another Key Idea. The equation must also contain the variable ω, so that we can set it to 0 and then solve for the corresponding time t. We choose Eq. 10-12, which yields
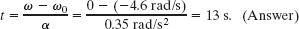
While you are operating a Rotor (the rotating cylindrical ride discussed in Sample Problem 6-8), you spot a passenger in acute distress and decrease the angular speed of the cylinder from 3.40 rad/s to 2.00 rad/s in 20.0 rev, at constant angular acceleration. (The passenger is obviously more of a “translation person” than a “rotation person.”)
(a) What is the constant angular acceleration during this decrease in angular speed?
Solution: Assume that the rotation is in the counterclockwise direction, and let the acceleration begin at time t = 0, at angular position θ0. The Key Idea here is that, because the cylinder’s angular acceleration is constant, we can relate it to the angular velocity and angular displacement via the basic equations for constant angular acceleration (Eqs. 10-12 and 10-13). The initial angular velocity is ω0 = 3.40 rad/s, the angular displacement is θ − θ0 = 20.0 rev, and the angular velocity at the end of that displacement is ω = 2.00 rad/s. But we do not know the angular acceleration α and time t, which are in both basic equations.
To eliminate the unknown t, we use Eq. 10-12 to write
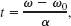
which we then substitute into Eq. 10-13 to write
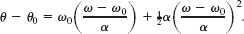
Solving for α, substituting known data, and converting 20 rev to 125.7 rad, we find
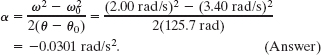
(b) How much time did the speed decrease take?
Solution: Now that we know α, we can use Eq. 10-12 to solve for t:
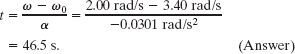
This sample problem is actually an angular version of Sample Problem 2-5. The data and symbols differ, but the techniques of solution are identical.
Leave a Reply