In Section 4-7, we discussed uniform circular motion, in which a particle travels at constant linear speed ν along a circle and around an axis of rotation. When a rigid body, such as a merry-go-round, rotates around an axis, each particle in the body moves in its own circle around that axis. Since the body is rigid, all the particles make one revolution in the same amount of time; that is, they all have the same angular speed ω.
However, the farther a particle is from the axis, the greater the circumference of its circle is, and so the faster its linear speed ν must be. You can notice this on a merry-go-round. You turn with the same angular speed ω regardless of your distance from the center, but your linear speed ν increases noticeably if you move to the outside edge of the merry-go-round.
We often need to relate the linear variables s, v, and a for a particular point in a rotating body to the angular variables θ, ω, and α for that body. The two sets of variables are related by r, the perpendicular distance of the point from the rotation axis. This perpendicular distance is the distance between the point and the rotation axis, measured along a perpendicular to the axis. It is also the radius r of the circle traveled by the point around the axis of rotation.
The Position
If a reference line on a rigid body rotates through an angle θ, a point within the body at a position r from the rotation axis moves a distance s along a circular arc, where s is given by Eq. 10-1:
This is the first of our linear–angular relations. Caution: The angle θ here must be measured in radians because Eq. 10-17 is itself the definition of angular measure in radians.
The Speed
Differentiating Eq. 10-17 with respect to time—with r held constant—leads to
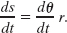
However, ds/dt is the linear speed (the magnitude of the linear velocity) of the point in question, and dθ/dt is the angular speed ω of the rotating body. So
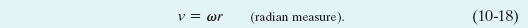
Caution: The angular speed ω must be expressed in radian measure.
Equation 10-18 tells us that since all points within the rigid body have the same angular speed ω, points with greater radius r have greater linear speed v. Figure 10-9a reminds us that the linear velocity is always tangent to the circular path of the point in question.
If the angular speed ω of the rigid body is constant, then Eq. 10-18 tells us that the linear speed v of any point within it is also constant. Thus, each point within the body undergoes uniform circular motion. The period of revolution T for the motion of each point and for the rigid body itself is given by Eq. 4-35:
This equation tells us that the time for one revolution is the distance 2π r traveled in one revolution divided by the speed at which that distance is traveled. Substituting for v from Eq. 10-18 and canceling r, we find also that
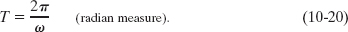
This equivalent equation says that the time for one revolution is the angular distance 2π rad traveled in one revolution divided by the angular speed (or rate) at which that angle is traveled.
The Acceleration
Differentiating Eq. 10-18 with respect to time—again with r held constant— leads to
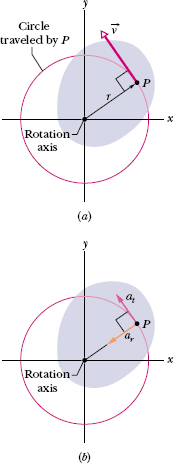
Fig. 10-9 The rotating rigid body of Fig. 10-2, shown in cross section viewed from above. Every point of the body (such as P) moves in a circle around the rotation axis. (a) The linear velocity 
of every point is tangent to the circle in which the point moves. (b) The linear acceleration 
of the point has (in general) two components: tangential at and radial ar.
Here we run up against a complication. In Eq. 10-21, dv/dt represents only the part of the linear acceleration that is responsible for changes in the magnitude v of the linear velocity . Like , that part of the linear acceleration is tangent to the path of the point in question. We call it the tangential component at of the linear acceleration of the point, and we write
where α = dω/dt. Caution: The angular acceleration α in Eq. 10-22 must be expressed in radian measure.
In addition, as Eq. 4-34 tells us, a particle (or point) moving in a circular path has a radial component of linear acceleration, ar = v2/r (directed radially inward), that is responsible for changes in the direction of the linear velocity . By substituting for v from Eq. 10-18, we can write this component as
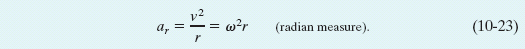
Thus, as Fig. 10-9b shows, the linear acceleration of a point on a rotating rigid body has, in general, two components. The radially inward component ar (given by Eq. 10-23) is present whenever the angular velocity of the body is not zero. The tangential component at (given by Eq. 10-22) is present whenever the angular acceleration is not zero.
CHECK POINT 3 A cockroach rides the rim of a rotating merry-go-round. If the angular speed of this system (merry-go-round + cockroach) is constant, does the cockroach have (a) radial acceleration and (b) tangential acceleration? If ω is decreasing, does the cockroach have (c) radial acceleration and (d) tangential acceleration?
We are to design the track for an induction roller coaster (which can be accelerated by magnetic forces even on a horizontal track). To create an initial thrill, we want each passenger to leave the loading point with acceleration g along the horizontal track. To increase the thrill, we also want that first section of track to form a circular arc (Fig. 10-10), so that the passenger also experiences a centripetal acceleration. As the passenger accelerates along the arc, the magnitude of this centripetal acceleration increases alarmingly. When the magnitude a of the net acceleration reaches 4g at some point P and angle θP along the arc, we want the passenger then to move in a straight line, along a tangent to the arc.
(a) What angle θP should the arc subtend so that a is 4g at point P?
Solution: One Key Idea here is that at any given time, the passenger’s net acceleration is the vector sum of the tangential acceleration 
along the track and the radial acceleration 
toward the arc’s center of curvature (as in Fig. 10-9b). Because and are perpendicular vectors, their sum has the magnitude
The value of at is set at g = 9.8 m/s2.
A second Key Idea is that the value of ar at any given time depends on the angular speed ω just then, according to Eq. 10-23:
where r is the radius of the circular arc.
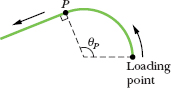
Fig. 10-10 An overhead view of a horizontal track for a roller coaster. The track begins as a circular arc at the loading point and then, at point P, continues along a tangent to the arc.
At the loading point, the passenger has an initial angular speed ω0 = 0 and initial angular position θ0 = 0. As the passenger accelerates along the track, the rate at which ω increases is the angular acceleration α. A third Key Idea is that, from Eq. 10-22, we can relate α to at:
Because both at and r are constant, α is constant, too. Thus a fourth Key Idea is that we can use the equations in Table 10-1. Because we are trying to determine a value for angular position θ, let us choose Eq. 10-14:
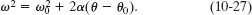
Substituting ω0 = 0, θ0 = 0, and α = at/r gives us
Substituting this result for ω2 into Eq. 10-25 yields
Next, substituting this result for ar into Eq. 10-24 and solving for θ lead to
When a reaches the design value of 4g, angle θ is the angle θP we want. Substituting a = 4g, θ = θP, and at = g into Eq. 10-30, we find
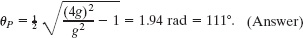
(b) What is the magnitude a of the passenger’s net acceleration at point P and after point P?
Solution: At P, a has the design value of 4g. Just after P is reached, the Key Idea is that the passenger moves in a straight line and no longer has centripetal acceleration. Thus, the passenger has only the acceleration magnitude g along the track. Hence,
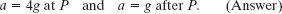
Roller-coaster headache can occur when a passenger’s head undergoes an abrupt change in acceleration, with the acceleration magnitude large before or after the change. The reason is that the change can cause the brain to move relative to the skull, tearing the veins that bridge the brain and skull. Our design to increase the acceleration from g to 4g along the path to P might harm the passenger, but the abrupt change in acceleration as the passenger passes through point P is more likely to cause roller-coaster headache.
PROBLEM – SOLVING TACTICS
TACTIC 1 : Units for Angular Variables
In Eq. 10-1 (θ = s/r), we began the use of radian measure for all angular variables whenever we are using equations that contain both angular and linear variables. Thus, we must express angular displacements in radians, angular velocities in rad/s and rad/min, and angular accelerations in rad/s2 and rad/min2. Equations 10-17, 10-18, 10-20, 10-22, and 10-23 are marked to emphasize this. The only exceptions to this rule are equations that involve only angular variables, such as the angular equations listed in Table 10-1. Here you are free to use any unit you wish for the angular variables; that is, you may use radians, degrees, or revolutions, as long as you use them consistently.
In equations where radian measure must be used, you need not keep track of the unit “radian” (rad) algebraically, as you must do for other units. You can add or delete it at will, to suit the context.
Leave a Reply