To locate an object means to find its position relative to some reference point, often the origin (or zero point) of an axis such as the x axis in Fig. 2-1. The positive direction of the axis is in the direction of increasing numbers (coordinates), which is to the right in Fig. 2-1. The opposite is the negative direction.
For example, a particle might be located at x = 5 m, which means it is 5 m in the positive direction from the origin. If it were at x = −5 m, it would be just as far from the origin but in the opposite direction. On the axis, a coordinate of −5 m is less than a coordinate of −1 m, and both coordinates are less than a coordinate of +5 m. A plus sign for a coordinate need not be shown, but a minus sign must always be shown.
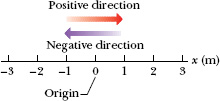
Fig. 2-1 Position is determined on an axis that is marked in units of length (here meters) and that extends indefinitely in opposite directions. The axis name, here x, is always on the positive side of the origin.
A change from one position x1 to another position x2 is called a displacement Δx, where
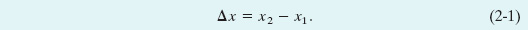
(The symbol Δ, the Greek uppercase delta, represents a change in a quantity, and it means the final value of that quantity minus the initial value.) When numbers are inserted for the position values x1 and x2 in Eq. 2-1, a displacement in the positive direction (to the right in Fig. 2-1) always comes out positive, and a displacement in the opposite direction (left in the figure) always comes out negative. For example, if the particle moves from x1 = 5 m to x2 = 12 m, then Δx = (12 m) − (5 m) = +7 m. The positive result indicates that the motion is in the positive direction. If, instead, the particle moves from x1 = 5 m to x2 = 1 m, then Δx = (1 m) − (5 m) = −4 m. The negative result indicates that the motion is in the negative direction.
The actual number of meters covered for a trip is irrelevant; displacement involves only the original and final positions. For example, if the particle moves from x = 5 m out to x = 200 m and then back to x = 5 m, the displacement from start to finish is Δx = (5 m) − (5 m) = 0.
A plus sign for a displacement need not be shown, but a minus sign must always be shown. If we ignore the sign (and thus the direction) of a displacement, we are left with the magnitude (or absolute value) of the displacement. For example, a displacement of Δx = −4 m has a magnitude of 4 m.
Displacement is an example of a vector quantity, which is a quantity that has both a direction and a magnitude. We explore vectors more fully in Chapter 3 (in fact, some of you may have already read that chapter), but here all we need is the idea that displacement has two features: (1) Its magnitude is the distance (such as the number of meters) between the original and final positions. (2) Its direction, from an original position to a final position, can be represented by a plus sign or a minus sign if the motion is along a single axis.
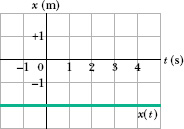
Fig. 2-2 The graph of x(t) for an armadillo that is stationary at x = −2 m. The value of x is −2 m for all times t.
What follows is the first of many checkpoints you will see in this book. Each consists of one or more questions whose answers require some reasoning or a mental calculation, and each gives you a quick check of your understanding of a point just discussed. The answers are listed in the back of the book.
![]() CHECKPOINT 1 Here are three pairs of initial and final positions, respectively, along an x axis. Which pairs give a negative displacement: (a) −3 m, +5 m; (b) −3 m, −7 m; (c) 7 m, −3 m?
CHECKPOINT 1 Here are three pairs of initial and final positions, respectively, along an x axis. Which pairs give a negative displacement: (a) −3 m, +5 m; (b) −3 m, −7 m; (c) 7 m, −3 m?
Leave a Reply