Everyday experience tells us that a given force produces different magnitudes of acceleration for different bodies. Put a baseball and a bowling ball on the floor and give both the same sharp kick. Even if you don’t actually do this, you know the result: The baseball receives a noticeably larger acceleration than the bowling ball. The two accelerations differ because the mass of the baseball differs from the mass of the bowling ball—but what, exactly, is mass?
We can explain how to measure mass by imagining a series of experiments in an inertial frame. In the first experiment we exert a force on a standard body, whose mass m0 is defined to be 1.0 kg. Suppose that the standard body accelerates at 1.0 m/s2. We can then say the force on that body is 1.0 N.
We next apply that same force (we would need some way of being certain it is the same force) to a second body, body X, whose mass is not known. Suppose we find that this body X accelerates at 0.25 m/s2. We know that a less massive baseball receives a greater acceleration than a more massive bowling ball when the same force (kick) is applied to both. Let us then make the following conjecture: The ratio of the masses of two bodies is equal to the inverse of the ratio of their accelerations when the same force is applied to both. For body X and the standard body, this tells us that
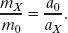
Solving for mX yields
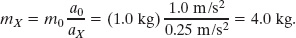
Our conjecture will be useful, of course, only if it continues to hold when we change the applied force to other values. For example, if we apply an 8.0 N force to the standard body, we obtain an acceleration of 8.0 m/s2. When the 8.0 N force is applied to body X, we obtain an acceleration of 2.0 m/s2. Our conjecture then gives us
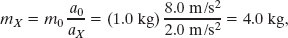
consistent with our first experiment. Many experiments yielding similar results indicate that our conjecture provides a consistent and reliable means of assigning a mass to any given body.
Our measurement experiments indicate that mass is an intrinsic characteristic of a body—that is, a characteristic that automatically comes with the existence of the body. They also indicate that mass is a scalar quantity. However, the nagging question remains: What, exactly, is mass?
Since the word mass is used in everyday English, we should have some intuitive understanding of it, maybe something that we can physically sense. Is it a body’s size, weight, or density? The answer is no, although those characteristics are sometimes confused with mass. We can say only that the mass of a body is the characteristic that relates a force on the body to the resulting acceleration. Mass has no more familiar definition; you can have a physical sensation of mass only when you attempt to accelerate a body, as in the kicking of a baseball or a bowling ball.
Leave a Reply