Force

We now wish to define the unit of force. We know that a force can cause the acceleration of a body. Thus, we shall define the unit of force in terms of the acceleration that a force gives to a standard reference body, which we take to be the standard kilogram of Fig. 1-4. This body has been assigned, exactly and by definition, a mass of 1 kg.

We put the standard body on a horizontal frictionless table and pull the body to the right (Fig. 5-1) so that, by trial and error, it eventually experiences a measured acceleration of 1 m/s². We then declare, as a matter of definition, that the force we are exerting on the standard body has a magnitude of 1 newton (abbreviated N).

We can exert a 2 N force on our standard body by pulling it so that its measured acceleration is 2 m/s², and so on. Thus in general, if our standard body of 1 kg mass has an acceleration of magnitude a, we know that a force F must be acting on it and that the magnitude of the force (in newtons) is equal to the magnitude of the acceleration (in meters per second per second).

Thus, a force is measured by the acceleration it produces. However, acceleration is a vector quantity, with both magnitude and direction. Is force also a vector quantity? We can easily assign a direction to a force (just assign the direction of the acceleration), but that is not sufficient. We must prove by experiment that forces are vector quantities. Actually, that has been done: forces are indeed vector quantities; they have magnitudes and directions, and they combine according to the vector rules of Chapter 3.

This means that when two or more forces act on a body, we can find their net force, or resultant force, by adding the individual forces vectorially. A single force that has the magnitude and direction of the net force has the same effect on the body as all the individual forces together. This fact is called the principle of superposition for forces. The world would be quite strange if, for example, you and a friend were to pull on the standard body in the same direction, each with a force of 1 N, and yet somehow the net pull was 14 N.

In this book, forces are most often represented with a vector symbol such as , and a net force is represented with the vector symbol . As with other vectors, a force or a net force can have components along coordinate axes. When forces act only along a single axis, they are single-component forces. Then we can drop the overhead arrows on the force symbols and just use signs to indicate the directions of the forces along that axis.

Instead of the wording used in Section 5-3, the more proper statement of Newton’s First Law is in terms of a net force:

 Newton’s First Law: If no net force acts on a body (), the body’s velocity cannot change; that is, the body cannot accelerate.

There may be multiple forces acting on a body, but if their net force is zero, the body cannot accelerate.

Inertial Reference Frames

Newton’s first law is not true in all reference frames, but we can always find reference frames in which it (as well as the rest of Newtonian mechanics) is true. Such frames are called inertial reference frames, or simply inertial frames.

 An inertial reference frame is one in which Newton’s laws hold.

For example, we can assume that the ground is an inertial frame provided we can neglect Earth’s astronomical motions (such as its rotation).

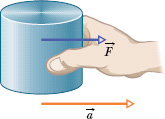
Fig. 5-1 A force  on the standard kilogram gives that body an acceleration .

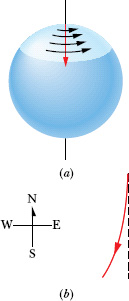
Fig. 5-2 (a) The path of a puck sliding from the north pole as seen from a stationary point in space. Earth rotates to the east. (b) The path of the pack as seen from the ground.

That assumption works well if, say, a puck is sent sliding along a short strip of frictionless ice—we would find that the puck’s motion obeys Newton’s laws. However, suppose the puck is sent sliding along a long ice strip extending from the north pole (Fig. 5-2a). If we view the puck from a stationary frame in space, the puck moves south along a simple straight line because Earth’s rotation around the north pole merely slides the ice beneath the puck. However, if we view the puck from a point on the ground so that we rotate with Earth, the puck’s path is not a simple straight line. Because the eastward speed of the ground beneath the puck is greater the farther south the puck slides, from our ground-based view the puck appears to be deflected westward (Fig. 5-2b). However, this apparent deflection is caused not by a force as required by Newton’s laws but by the fact that we see the puck from a rotating frame. In this situation, the ground is a noninertial frame.

In this book we usually assume that the ground is an inertial frame and that measured forces and accelerations are from this frame. If measurements are made in, say, an elevator that is accelerating relative to the ground, then the measurements are being made in a noninertial frame and the results can be surprising. We see an example of this in Sample Problem 5-8.

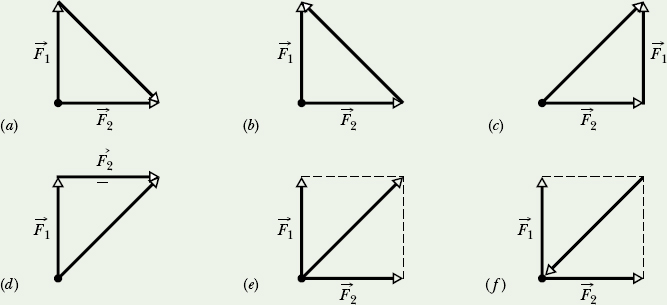
 CHECKPOINT 1 Which of the figure’s six arrangements correctly show the vector addition of forces  and  to yield the third vector, which is meant to represent their net force ?