Elastic Collisions in One Dimension

As we discussed in Section 9-8, everyday collisions are inelastic but we can approximate some of them as being elastic; that is, we can approximate that the total kinetic energy of the colliding bodies is conserved and is not transferred to other forms of energy:

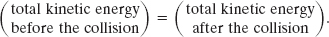
This does not mean that the kinetic energy of each colliding body cannot change. Rather, it means this:

 In an elastic collision, the kinetic energy of each colliding body may change, but the total kinetic energy of the system does not change.

For example, the collision of a cue ball with an object ball in a game of pool can be approximated as being an elastic collision. If the collision is head-on (the cue ball heads directly toward the object ball), the kinetic energy of the cue ball can be transferred almost entirely to the object ball. (Still, the fact that the collision makes a sound means that at least a little of the kinetic energy is transferred to the energy of the sound.)

Stationary Target

Figure 9-19 shows two bodies before and after they have a one-dimensional collision, like a head-on collision between pool balls. A projectile body of mass m₁ and initial velocity v_1i moves toward a target body of mass m₂ that is initially at rest (v_2i = 0). Let’s assume that this two-body system is closed and isolated. Then the net linear momentum of the system is conserved, and from Eq. 9-51 we can write that conservation as

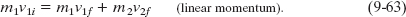
If the collision is also elastic, then the total kinetic energy is conserved and we can write that conservation as

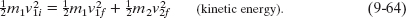
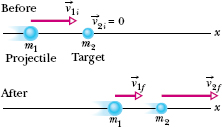
Fig. 9-19   Body 1 moves along an x axis before having an elastic collision with body 2, which is initially at rest. Both bodies move along that axis after the collision.

In each of these equations, the subscript i identifies the initial velocities and the subscript f the final velocities of the bodies. If we know the masses of the bodies and if we also know v_1i, the initial velocity of body 1, the only unknown quantities are v_1f and v_2f, the final velocities of the two bodies. With two equations at our disposal, we should be able to find these two unknowns.

To do so, we rewrite Eq. 9-63 as

and Eq. 9-64 as*

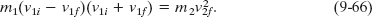
After dividing Eq. 9-66 by Eq. 9-65 and doing some more algebra, we obtain

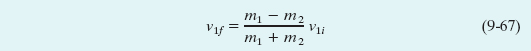
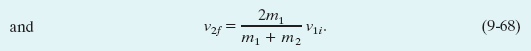
We note from Eq. 9-68 that v_2f is always positive (the initially stationary target body with mass m₂ always moves forward). From Eq. 9-67 we see that v_1f may be of either sign (the projectile body with mass m₁ moves forward if m₁ > m₂ but rebounds if m₁ < m₂).

Let us look at a few special situations.

1.  Equal masses   If m₁ = m₂, Eqs. 9-67 and 9-68 reduce to

v_1f = 0  and  v_2f = v_1i,

which we might call a pool player’s result. It predicts that after a head-on collision of bodies with equal masses, body 1 (initially moving) stops dead in its tracks and body 2 (initially at rest) takes off with the initial speed of body 1. In head-on collisions, bodies of equal mass simply exchange velocities. This is true even if body 2 is not initially at rest.

2.  A massive target  In Fig. 9-19, a massive target means that m₂  m₁. For example, we might fire a golf ball at a stationary cannonball. Equations 9-67 and 9-68 then reduce to

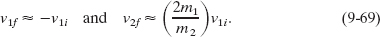
This tells us that body 1 (the golf ball) simply bounces back along its incoming path, its speed essentially unchanged. Initially stationary body 2 (the cannonball) moves forward at a low speed, because the quantity in parentheses in Eq. 9-69 is much less than unity. All this is what we should expect.

3.  A massive projectile  This is the opposite case; that is, m₁  m₂. This time, we fire a cannonball at a stationary golf ball. Equations 9-67 and 9-68 reduce to

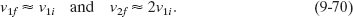
Equation 9-70 tells us that body 1 (the cannonball) simply keeps on going, scarcely slowed by the collision. Body 2 (the golf ball) charges ahead at twice the speed of the cannonball.

You may wonder: Why twice the speed? As a starting point in thinking about the matter, recall the collision described by Eq. 9-69, in which the velocity of the incident light body (the golf ball) changed from +v to −v, a velocity change of 2v. The same change in velocity (but now from zero to 2v) occurs in this example also.

Moving Target

Now that we have examined the elastic collision of a projectile and a stationary target, let us examine the situation in which both bodies are moving before they undergo an elastic collision.

Fig. 9-20   Two bodies headed for a one-dimensional elastic collision.

For the situation of Fig. 9-20, the conservation of linear momentum is written as

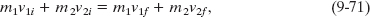
and the conservation of kinetic energy is written as

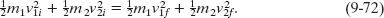
To solve these simultaneous equations for v_1f and v_2f, we first rewrite Eq. 9-71 as

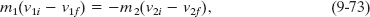
and Eq. 9-72 as

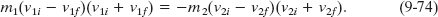
After dividing Eq. 9-74 by Eq. 9-73 and doing some more algebra, we obtain

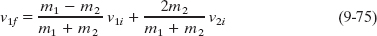
and

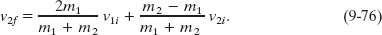
Note that the assignment of subscripts 1 and 2 to the bodies is arbitrary. If we exchange those subscripts in Fig. 9-20 and in Eqs. 9-75 and 9-76, we end up with the same set of equations. Note also that if we set v_2i = 0, body 2 becomes a stationary target as in Fig. 9-19, and Eqs. 9-75 and 9-76 reduce to Eqs. 9-67 and 9-68, respectively.

 CHECKPOINT 10   What is the final linear momentum of the target in Fig. 9-19 if the initial linear momentum of the projectile is 6 kg · m/s and the final linear momentum of the projectile is (a) 2 kg · m/s and (b) −2 kg · m/s? (c) What is the final kinetic energy of the target if the initial and final kinetic energies of the projectile are, respectively, 5 J and 2 J?

Sample Problem 9-10

Two metal spheres, suspended by vertical cords, initially just touch, as shown in Fig. 9-21. Sphere 1, with mass m₁ = 30 g, is pulled to the left to height h₁ = 8.0 cm, and then released from rest. After swinging down, it undergoes an elastic collision with sphere 2, whose mass m₂ = 75 g. What is the velocity v_1f of sphere 1 just after the collision?

Solution: A first Key Idea is that we can split this complicated motion into two steps that we can analyze separately: (1) the descent of sphere 1 and (2) the two-sphere collision.

Step 1  The Key Idea here is that as sphere 1 swings down, the mechanical energy of the sphere–Earth system is conserved. (The mechanical energy is not changed by the force of the cord on sphere 1 because that force is always directed perpendicular to the sphere’s direction of travel.) Let’s take the lowest level as our reference level of zero gravitational potential energy. Then the kinetic energy of sphere 1 at the lowest level must equal the gravitational potential energy of the system when sphere 1 is at height h₁. Thus,

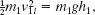
which we solve for the speed v_1i of sphere 1 just before the collision:

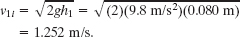
Step 2  Here we can make two assumptions in addition to the assumption that the collision is elastic. First, we can assume that the collision is one-dimensional because the motions of the spheres are approximately horizontal from just before the collision to just after it. Second, because the collision is so brief, we can assume that the two-sphere system is closed and isolated. This gives the Key Idea that the total linear momentum of the system is conserved. Thus, we can use Eq. 9-67 to find the velocity of sphere 1 just after the collision:

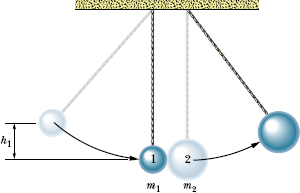
Fig. 9-21   Two metal spheres suspended by cords just touch when they are at rest. Sphere 1, with mass m₁, is pulled to the left to height h₁ and then released.

The minus sign tells us that sphere 1 moves to the left just after the collision.