Here we find equations that give the value of the two types of potential energy discussed in this chapter: gravitational potential energy and elastic potential energy. However, first we must find a general relation between a conservative force and the associated potential energy.
Consider a particle-like object that is part of a system in which a conservative force ![]() acts. When that force does work W on the object, the change ΔU in the potential energy associated with the system is the negative of the work done. We wrote this fact as Eq. 8-1 (ΔU = −W). For the most general case, in which the force may vary with position, we may write the work W as in Eq. 7-32:
acts. When that force does work W on the object, the change ΔU in the potential energy associated with the system is the negative of the work done. We wrote this fact as Eq. 8-1 (ΔU = −W). For the most general case, in which the force may vary with position, we may write the work W as in Eq. 7-32:

This equation gives the work done by the force when the object moves from point xi to point xf, changing the configuration of the system. (Because the force is conservative, the work is the same for all paths between those two points.)
Substituting Eq. 8-5 into Eq. 8-1, we find that the change in potential energy due to the change in configuration is

This is the general relation we sought. Let’s put it to use.
Gravitational Potential Energy
We first consider a particle with mass m moving vertically along a y axis (the positive direction is upward). As the particle moves from point yi to point yf, the gravitational force ![]() does work on it. To find the corresponding change in the gravitational potential energy of the particle—Earth system, we use Eq. 8-6 with two changes: (1) We integrate along the y axis instead of the x axis, because the gravitational force acts vertically. (2) We substitute –mg for the force symbol F, because
does work on it. To find the corresponding change in the gravitational potential energy of the particle—Earth system, we use Eq. 8-6 with two changes: (1) We integrate along the y axis instead of the x axis, because the gravitational force acts vertically. (2) We substitute –mg for the force symbol F, because ![]() has the magnitude mg and is directed down the y axis. We then have
has the magnitude mg and is directed down the y axis. We then have
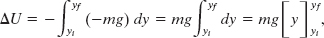
which yields
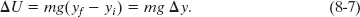
Only changes ΔU in gravitational potential energy (or any other type of potential energy) are physically meaningful. However, to simplify a calculation or a discussion, we sometimes would like to say that a certain gravitational potential value U is associated with a certain particle – Earth system when the particle is at a certain height y. To do so, we rewrite Eq. 8-7 as

Then we take Ui to be the gravitational potential energy of the system when it is in a reference configuration in which the particle is at a reference point yi. Usually we take Ui = 0 and yi = 0. Doing this changes Eq. 8-8 to

This equation tells us:
![]() The gravitational potential energy associated with a particle–Earth system depends only on the vertical position y (or height) of the particle relative to the reference position y = 0, not on the horizontal position.
The gravitational potential energy associated with a particle–Earth system depends only on the vertical position y (or height) of the particle relative to the reference position y = 0, not on the horizontal position.
Elastic Potential Energy
We next consider the block – spring system shown in Fig. 8-3, with the block moving on the end of a spring of spring constant k. As the block moves from point xi to point xf, the spring force Fx = −kx does work on the block. To find the corresponding change in the elastic potential energy of the block – spring system, we substitute − kx for F(x) in Eq. 8-6. We then have
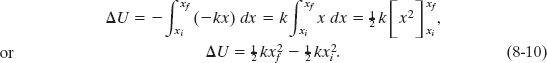
To associate a potential energy value U with the block at position x, we choose the reference configuration to be when the spring is at its relaxed length and the block is at xi = 0. Then the elastic potential energy Ui is 0, and Eq. 8-10 becomes
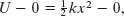
which gives us

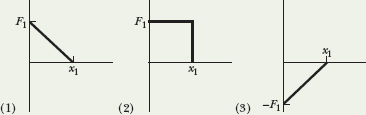
![]() CHECK POINT 2 A particle is to move along an x axis from x = 0 to x1 while a conservative force, directed along the x axis, acts on the particle. The figure shows three situations in which the x component of that force varies with x. The force has the same maximum magnitude F1 in all three situations. Rank the situations according to the change in the associated potential energy during the particle’s motion, most positive first.
CHECK POINT 2 A particle is to move along an x axis from x = 0 to x1 while a conservative force, directed along the x axis, acts on the particle. The figure shows three situations in which the x component of that force varies with x. The force has the same maximum magnitude F1 in all three situations. Rank the situations according to the change in the associated potential energy during the particle’s motion, most positive first.
TACTIC 1: Using the Term “Potential Energy”
A potential energy is associated with a system as a whole. However, you might see statements that associate it with only part of the system. For example, you might read, “An apple hanging in a tree has a gravitational potential energy of 30 J.” Such statements are often acceptable, but you should always keep in mind that the potential energy is actually associated with a system—here the apple–Earth system. Also keep in mind that assigning a particular potential energy value, such as 30 J here, to an object or even a system makes sense only if the reference potential energy value is known, as explored in Sample Problem 8-2.
A 2.0 kg sloth hangs 5.0 m above the ground (Fig. 8-6).
(a) What is the gravitational potential energy U of the sloth–Earth system if we take the reference point y = 0 to be (1) at the ground, (2) at a balcony floor that is 3.0 m above the ground, (3) at the limb, and (4) 1.0 m above the limb? Take the gravitational potential energy to be zero at y = 0.
Solution: The Key Idea here is that once we have chosen the reference point for y = 0, we can calculate the gravitational potential energy U of the system relative to that reference point with Eq. 8-9. For example, for choice (1) the sloth is at y = 5.0 m, and
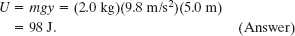
For the other choices, the values of U are
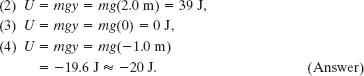
(b) The sloth drops to the ground. For each choice of reference point, what is the change ΔU in the potential energy of the sloth–Earth system due to the fall?
Solution: The Key Idea here is that the change in potential energy does not depend on the choice of the reference point for y = 0; instead, it depends on the change in height Δy. For all four situations, we have the same Δy = − 5.0 m. Thus, for
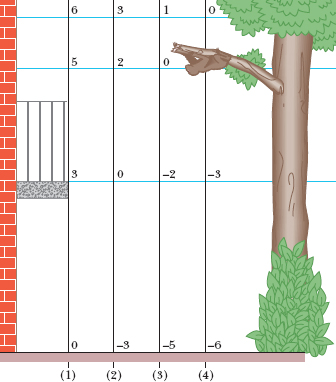
Fig. 8-6 Four choices of reference point y = 0. Each y axis is marked in units of meters. The choice affects the value of the potential energy U of the sloth–Earth system. However, it does not affect the change ΔU in potential energy of the system if the sloth moves by, say, falling.
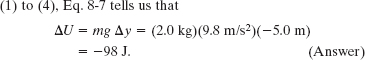
Leave a Reply