Suppose that the net external force 
(and thus the net impulse 
) acting on a system of particles is zero (the system is isolated) and that no particles leave or enter the system (the system is closed). Putting 
in Eq. 9-27 then yields 
or
In words,
If no net external force acts on a system of particles, the total linear momentum 
of the system cannot change.
This result is called the law of conservation of linear momentum. It can also be written as
In words, this equation says that, for a closed, isolated system,
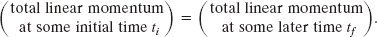
Caution: Momentum should not be confused with energy. In the sample problems of this section, momentum is conserved but energy is definitely not.
Equations 9-42 and 9-43 are vector equations and, as such, each is equivalent to three equations corresponding to the conservation of linear momentum in three mutually perpendicular directions as in, say, an xyz coordinate system. Depending on the forces acting on a system, linear momentum might be conserved in one or two directions but not in all directions. However,
If the component of the net external force on a closed system is zero along an axis, then the component of the linear momentum of the system along that axis cannot change.
As an example, suppose that you toss a grapefruit across a room. During its flight, the only external force acting on the grapefruit (which we take as the system) is the gravitational force 
, which is directed vertically downward. Thus, the vertical component of the linear momentum of the grapefruit changes, but since no horizontal external force acts on the grapefruit, the horizontal component of the linear momentum cannot change.
Note that we focus on the external forces acting on a closed system. Although internal forces can change the linear momentum of portions of the system, they cannot change the total linear momentum of the entire system.
The sample problems in this section involve explosions that are either one-dimensional (meaning that the motions before and after the explosion are along a single axis) or two-dimensional (meaning that they are in a plane containing two axes). In the following sections we consider one-dimensional and two-dimensional collisions.
CHECKPOINT 6 An initially stationary device lying on a frictionless floor explodes into two pieces, which then slide across the floor. One piece slides in the positive direction of an x axis. (a) What is the sum of the momenta of the two pieces after the explosion? (b) Can the second piece move at an angle to the x axis? (c) What is the direction of the momentum of the second piece?
One-dimensional explosion: A ballot box with mass m = 6.0 kg slides with speed v = 4.0 m/s across a frictionless floor in the positive direction of an x axis. The box explodes into two pieces. One piece, with mass m1 = 2.0 kg, moves in the positive direction of the x axis at v1 = 8.0 m/s. What is the velocity of the second piece, with mass m2?
Solution: There are two Key Ideas. We could get the velocity of the second piece if we knew its momentum, because we already know its mass is m2 = m − m1 = 4.0 kg. We can relate the momenta of the two pieces to the original momentum of the box if momentum is conserved. Let’s check.
Our reference frame will be that of the floor. Our system, which consists initially of the box and then of the two pieces, is closed but is not isolated, because the box and pieces each experience a normal force from the floor and a gravitational force. However, those forces are both vertical and thus cannot change the horizontal component of the momentum of the system. Neither can the forces produced by the explosion, because those forces are internal to the system. Thus, the horizontal component of the momentum of the system is conserved, and we can apply Eq. 9-43 along the x axis.
The initial momentum of the system is that of the box:
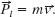
Similarly, we can write the final momenta of the two pieces as
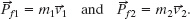
The final total momentum 
of the system is the vector sum of the momenta of the two pieces:
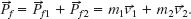
Since all the velocities and momenta in this problem are vectors along the x axis, we can write them in terms of their x components. Doing so while applying Eq. 9-43, we now obtain
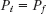
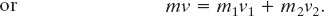
Inserting known data, we find
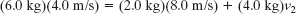
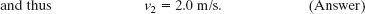
Since the result is positive, the second piece moves in the positive direction of the x axis.
One-dimensional explosion: Figure 9-12a shows a space hauler and cargo module, of total mass M, traveling along an x axis in deep space. They have an initial velocity 
of magnitude 2100 km/h relative to the Sun. With a small explosion, the hauler ejects the cargo module, of mass 0.20M (Fig. 9-12b). The hauler then travels 500 km/h faster than the module along the x axis; that is, the relative speed vrel between the hauler and the module is 500 km/h. What then is the velocity 
of the hauler relative to the Sun?
Solution: The Key Idea here is that, because the hauler–module system is closed and isolated, its total linear momentum is conserved; that is,
where the subscripts i and f refer to values before and after the ejection, respectively. Because the motion is along a single axis, we can write momenta and velocities in terms of their x components. Before the ejection, we have
Let vMS be the velocity of the ejected module relative to the Sun. The total linear momentum of the system after the ejection is then
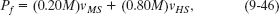
where the first term on the right is the linear momentum of the module and the second term is that of the hauler.
We do not know the velocity vMS of the module relative to the Sun, but we can relate it to the known velocities with
In symbols, this gives us
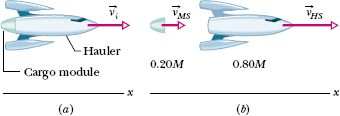
Fig. 9-12 (a) A space hauler, with a cargo module, moving at initial velocity . (b) The hauler has ejected the cargo module. Now the velocities relative to the Sun are 
for the module and for the hauler.
Substituting this expression for vMS into Eq. 9-46, and then substituting Eqs. 9-45 and 9-46 into Eq. 9-44, we find
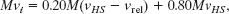
which gives us
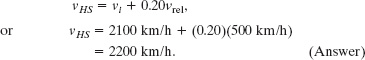
CHECKPOINT 7 The table gives velocities of the hauler and module (after ejection and relative to the Sun), and the relative speed between the hauler and the module for three situations. What are the missing values?
Two-dimensional explosion: A firecracker placed inside a coconut of mass M, initially at rest on a frictionless floor, blows the coconut into three pieces that slide across the floor. An overhead view is shown in Fig. 9-13a. Piece C, with mass 0.30M, has final speed vfC = 5.0 m/s.
(a) What is the speed of piece B, with mass 0.20M?
Solution: A Key Idea here is to see whether linear momentum is conserved. We note that (1) the coconut and its pieces form a closed system, (2) the explosion forces are internal to that system, and (3) no net external force acts on the system. Therefore, the linear momentum of the system is conserved.
To get started, we superimpose an xy coordinate system as shown in Fig. 9-13b, with the negative direction of the x axis coinciding with the direction of 
. The x axis is at 80° with the direction of 
and 50° with the direction of 
A second Key Idea is that linear momentum is conserved separately along each axis. Let’s use the y axis and write
where subscript i refers to the initial value (before the explosion), and subscript y refers to the y component of 
or 
.
The component Piy of the initial linear momentum is zero, because the coconut is initially at rest. To get an expression for Pfy, we find the y component of the final linear momentum of each piece, using the y-component version of Eq. 9-22 (py = mvy):
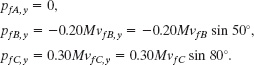
(Note that pfA,y = 0 because of our choice of axes.) Equation 9-48 can now be written as
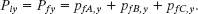
Then, with vfC = 5.0 m/s, we have
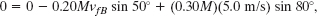
from which we find
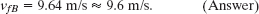
(b) What is the speed of piece A?
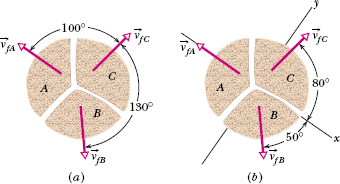
Fig. 9-13 Three pieces of an exploded coconut move off in three directions along a frictionless floor. (a) An overhead view of the event. (b) The same with a two-dimensional axis system imposed.
Solution: Because linear momentum is also conserved along the x axis, we have
where 
because the coconut is initially at rest. To get Pfx, we find the x components of the final momenta, using the fact that piece A must have a mass of 0.50M (= M − 0.20M − 0.30M):
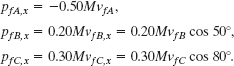
Equation 9-49 can now be written as
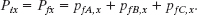
Then, with vfC = 5.0 m/s and vfB = 9.64 m/s, we have
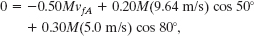
from which we find
CHECKPOINT 8 Suppose that the exploding coconut is accelerating in the negative direction of y in Fig. 9-13 (say it is on a ramp that slants downward in that direction). Is linear momentum conserved along (a) the x axis (as stated in Eq. 9-49) and (b) the y axis (as stated in Eq. 9-48)?
PROBLEM – SOLVING TACTICS
TACTIC 2: Conservation of Linear Momentum
For problems involving the conservation of linear momentum, first make sure that you have chosen a closed, isolated system. Closed means that no matter (no particles) passes through the system boundary in any direction. Isolated means that the net external force acting on the system is zero. If it is not isolated, then remember that each component of linear momentum is conserved separately if the corresponding component of the net external force is zero. So, you might conserve one component and not another.
Next, select two appropriate states of the system (which you may choose to call the initial state and the final state) and write expressions for the linear momentum of the system in each of these two states. In writing these expressions, make sure that you know what inertial reference frame you are using, and make sure also that you include the entire system, not missing any part of it and not including objects that do not belong to your system.
Finally, set your expressions for and equal to each other and solve for what is requested.
Leave a Reply