We often need to change the units in which a physical quantity is expressed. We do so by a method called chain-link conversion. In this method, we multiply the original measurement by a conversion factor (a ratio of units that is equal to unity). For example, because 1 min and 60 s are identical time intervals, we have
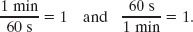
Thus, the ratios (1 min)/(60 s) and (60 s)/(1 min) can be used as conversion factors. This is not the same as writing ![]() = 1 or 60 = 1; each number and its unit must be treated together.
= 1 or 60 = 1; each number and its unit must be treated together.
Because multiplying any quantity by unity leaves the quantity unchanged, we can introduce conversion factors wherever we find them useful. In chain-link conversion, we use the factors to cancel unwanted units. For example, to convert 2 min to seconds, we have
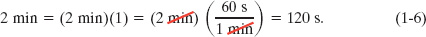
If you introduce a conversion factor in such a way that unwanted units do not cancel, invert the factor and try again. In conversions, the units obey the same algebraic rules as variables and numbers.
Appendix D gives conversion factors between SI and other systems of units, including non-SI units still used in the United States. However, the conversion factors are written in the style of “1 min = 60 s” rather than as a ratio. The following sample problem gives an example of how to set up such ratios.
When Pheidippides ran from Marathon to Athens in 490 B.C. to bring word of the Greek victory over the Persians, he probably ran at a speed of about 23 rides per hour (rides/h). The ride is an ancient Greek unit for length, as are the stadium and the plethron: 1 ride was defined to be 4 stadia, 1 stadium was defined to be 6 plethra, and, in terms of a modern unit, 1 plethron is 30.8 m. How fast did Pheidippides run in kilometers per second (km/s)?
Solution: The Key Idea in chain-link conversions is to write the conversion factors as ratios that will eliminate unwanted units. Here we write

The cran is a British volume unit for freshly caught herrings: 1 cran = 170.474 liters (L) of fish, about 750 herrings. Suppose that, to be cleared through customs in Saudia Arabia, a shipment of 1255 crans must be declared in terms of cubic covidos, where the covido is an Arabic unit of length: 1 covido = 48.26 cm. What is the required declaration?
Solution: From Appendix D we see that 1 L is equivalent to 1000 cm3. A Key Idea then helps: To convert from cubic centimeters to cubic covidos, we must cube the conversion ratio between centimeters and covidos. Thus, we write the following chain-link conversion:
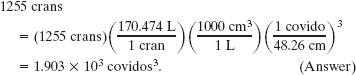
PROBLEM-SOLVING TACTICS
TACTIC1: Significant Figures and Decimal Places
If you calculated the answer to Sample Problem 1-1 without your calculator automatically rounding it off, the number 4.722 666 666 67 × 10−3 might have appeared in the display. The precision implied by this number is meaningless. We rounded the answer to 4.7 × 10−3 km/s so as not to imply that it is more precise than the given data. The given speed of 23 rides/h consists of two digits, called significant figures. Thus, we rounded the answer to two significant figures. In this book, final results of calculations are often rounded to match the least number of significant figures in the given data. (However, sometimes an extra significant figure is kept.) When the leftmost of the digits to be discarded is 5 or more, the last remaining digit is rounded up; otherwise it is retained as is. For example, 11.3516 is rounded to three significant figures as 11.4 and 11.3279 is rounded to three significant figures as 11.3. (The answers to sample problems in this book are usually presented with the symbol = instead of ≈ even if rounding is involved.)
When a number such as 3.15 or 3.15 × 10 is provided in a problem, the number of significant figures is apparent, but how about the number 3000? Is it known to only one signifi-cant figure (3 × 103)? Or is it known to as many as four significant figures (3.000 × 103)? In this book, we assume that all the zeros in such given numbers as 3000 are significant, but you had better not make that assumption elsewhere.
Don’t confuse significant figures with decimal places. Consider the lengths 35.6 mm, 3.56 m, and 0.00356 m. They all have three significant figures but they have one, two, and five decimal places, respectively.
Leave a Reply