If a particle moves from one point to another, we might need to know how fast it moves. Just as in Chapter 2, we can define two quantities that deal with “how fast”: average velocity and instantaneous velocity. However, here we must consider these quantities as vectors and use vector notation.
If a particle moves through a displacement Δ![]() in a time interval Δt, then its average velocity
in a time interval Δt, then its average velocity  avg is
avg is
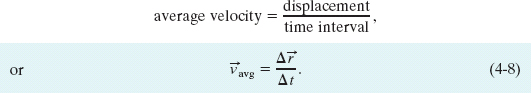
This tells us that the direction of  avg (the vector on the left side of Eq. 4-8) must be the same as that of the displacement Δ
avg (the vector on the left side of Eq. 4-8) must be the same as that of the displacement Δ![]() (the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
(the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
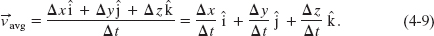
For example, if the particle in Sample Problem 4-1 moves from its initial position to its later position in 2.0 s, then its average velocity during that move is
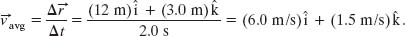
That is, the average velocity (a vector quantity) has a component of 6.0 m/s along the x axis and a component of 1.5 m/s along the z axis.
When we speak of the velocity of a particle, we usually mean the particle’s instantaneous velocity  at some instant. This
at some instant. This  is the value that
is the value that  avg approaches in the limit as we shrink the time interval Δt to 0 about that instant. Using the language of calculus, we may write
avg approaches in the limit as we shrink the time interval Δt to 0 about that instant. Using the language of calculus, we may write  as the derivative
as the derivative
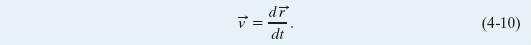
Figure 4-4 shows the path of a particle that is restricted to the xy plane. As the particle travels to the right along the curve, its position vector sweeps to the right. During time interval Δt, the position vector changes from ![]() 1 to
1 to ![]() 2 and the particle’s displacement is Δ
2 and the particle’s displacement is Δ![]() .
.
To find the instantaneous velocity of the particle at, say, instant t1 (when the particle is at position 1), we shrink interval Δt to 0 about t1. Three things happen as we do so. (1) Position vector ![]() 2 in Fig. 4-4 moves toward
2 in Fig. 4-4 moves toward ![]() 1 so that Δ
1 so that Δ![]() shrinks toward zero. (2) The direction of Δ
shrinks toward zero. (2) The direction of Δ![]() /Δt (and thus of
/Δt (and thus of  avg) approaches the direction of the line tangent to the particle’s path at position 1. (3) The average velocity
avg) approaches the direction of the line tangent to the particle’s path at position 1. (3) The average velocity  avg approaches the instantaneous velocity
avg approaches the instantaneous velocity  at t1.
at t1.
In the limit as Δt → 0, we have  avg →
avg →  and, most important here,
and, most important here,  avg takes on the direction of the tangent line. Thus,
avg takes on the direction of the tangent line. Thus,  has that direction as well:
has that direction as well:
![]() The direction of the instantaneous velocity
The direction of the instantaneous velocity ![]() of a particle is always tangent to the particle’s path at the particle’s position.
of a particle is always tangent to the particle’s path at the particle’s position.
The result is the same in three dimensions:  is always tangent to the particle’s path.
is always tangent to the particle’s path.
To write Eq. 4-10 in unit-vector form, we substitute for ![]() from Eq. 4-1:
from Eq. 4-1:
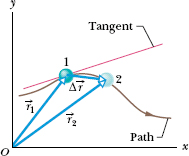
Fig. 4-4 The displacement Δ![]() of a particle during a time interval Δt, from position 1 with position vector
of a particle during a time interval Δt, from position 1 with position vector ![]() 1 at time t1 to position 2 with position vector
1 at time t1 to position 2 with position vector ![]() 2 at time t2. The tangent to the particle’s path at position 1 is shown.
2 at time t2. The tangent to the particle’s path at position 1 is shown.
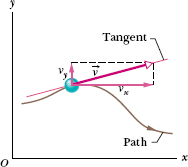
Fig. 4-5 The velocity  of a particle, along with the scalar components of
of a particle, along with the scalar components of  .
.
This equation can be simplified somewhat by writing it as
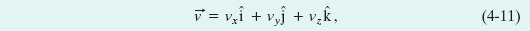
where the scalar components of  are
are
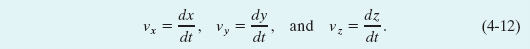
For example, dx/dt is the scalar component of  along the x axis. Thus, we can find the scalar components of
along the x axis. Thus, we can find the scalar components of  by differentiating the scalar components of
by differentiating the scalar components of ![]() .
.
Figure 4-5 shows a velocity vector  and its scalar x and y components. Note that
and its scalar x and y components. Note that  is tangent to the particle’s path at the particle’s position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-4, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn, as in Fig. 4-5, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its length (representing the velocity magnitude) can be drawn to any scale.
is tangent to the particle’s path at the particle’s position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-4, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn, as in Fig. 4-5, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its length (representing the velocity magnitude) can be drawn to any scale.
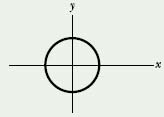
![]() CHECKPOINT 2 The figure shows a circular path taken by a particle. If the instantaneous velocity of the particle is
CHECKPOINT 2 The figure shows a circular path taken by a particle. If the instantaneous velocity of the particle is ![]() = (2 m/s)
= (2 m/s)![]() − (2 m/s)
− (2 m/s)![]() , through which quadrant is the particle moving at that instant if it is traveling (a) clockwise and (b) counterclockwise around the circle? For both cases, draw
, through which quadrant is the particle moving at that instant if it is traveling (a) clockwise and (b) counterclockwise around the circle? For both cases, draw ![]() on the figure.
on the figure.
For the rabbit in Sample Problem 4-2, find the velocity  at time t = 15 s, in unit-vector notation and in magnitude-angle notation.
at time t = 15 s, in unit-vector notation and in magnitude-angle notation.
Solution: There are two Key Ideas here: (1) We can find the rabbit’s velocity  by first finding the velocity components. (2) We can find those components by taking derivatives of the components of the rabbit’s position vector. Applying the vx part of Eq. 4-12 to Eq. 4-5, we find the x component of
by first finding the velocity components. (2) We can find those components by taking derivatives of the components of the rabbit’s position vector. Applying the vx part of Eq. 4-12 to Eq. 4-5, we find the x component of  to be
to be
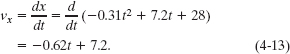
At t = 15 s, this gives vx = −2.1 m/s. Similarly, applying the vy part of Eq. 4-12 to Eq. 4-6, we find that the y component is
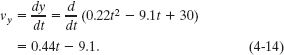
At t = 15 s, this gives vy = −2.5 m/s. Equation 4-11 then yields
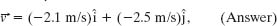
which is shown in Fig. 4-6, tangent to the rabbit’s path and in the direction the rabbit is running at t = 15 s.
To get the magnitude and angle of  , either we use a vector-capable calculator or we follow Eq. 3-6 to write
, either we use a vector-capable calculator or we follow Eq. 3-6 to write

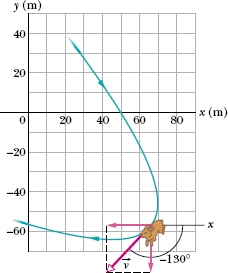
Fig. 4-6 The rabbit’s velocity  at t = 15 s. The velocity vector is tangent to the path at the rabbit’s position at that instant. The scalar components of
at t = 15 s. The velocity vector is tangent to the path at the rabbit’s position at that instant. The scalar components of  are shown.
are shown.
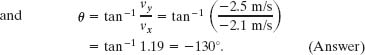
(Although 50° has the same tangent as −130°, inspection of the signs of the velocity components indicates that the desired angle is in the third quadrant, given by 50° − 180° = −130°.)
Leave a Reply