The purpose of this section is to help you understand and learn how to use Equation 3.17, the Butler–Volmer equation. The BV equation is a relationship between the current density (i) and the charge transfer or surface overpotential (η_s). It contains three parameters: the exchange-current density (i_o), the anodic charge transfer coefficient (α_a), and the cathodic charge transfer coefficient (α_c). It is frequently used to represent experimental data by fitting these three parameters to the data.

The charge transfer overpotential (η_s) is defined by Equation 3.15, where V represents the difference between the potential of the electrode (ϕ₁, often a metal) and the potential of a reference electrode located just outside the double layer (ϕ₂). U is the difference between the potential of the electrode and the reference electrode at equilibrium. As already mentioned, V and U must be relative to the same reference electrode, although the precise choice of reference electrode is not critical as long as it is appropriate for the system. Note that U = 0 if the reference electrode is the same as the electrode of interest. For example, U would be zero for the combination of a zinc electrode and a zinc reference electrode (Why?). The methods that you learned in Chapter 2 can be used to calculate U, which is a function of the concentration at the surface.

The current density (i) is the current per area, with typical units of mA·cm⁻² or A·m⁻². In theory, it is based on the actual area over which the reaction is taking place. The area, however, can be an issue in practice. For example, if the measured value of i_o is based on the superficial or apparent area in a system where the microscopic area is significantly greater than the superficial area, i_o will not transfer to another system with a different microstructure (see Figure 3.6). The surface roughness illustrated in Figure 3.6b results in a larger surface area for electrochemical reaction.

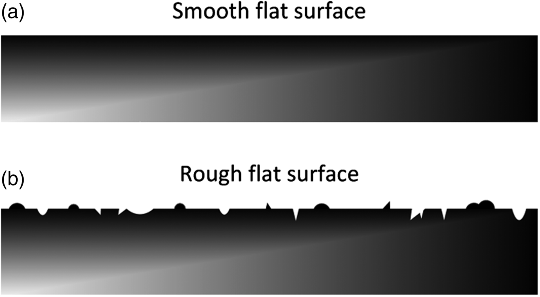
A surface roughness factor, R_a, can be defined as the ratio of the true surface area and the apparent surface area, a ratio that can be quite large. Consequently, care should be taken to accurately account for the area for which the current density is defined. We will consider this topic in some detail in Chapter 5, and in other places in the text.

The exchange-current density, i_o, represents the rate per area of the forward and reverse reactions at equilibrium, where the total current is zero (see Equation 3.16). The exchange-current density for different reactions can vary over many orders of magnitude, as shown in Table 3.1 for some commonly encountered reactions. The value of i_o for a given reaction can also vary widely as a function of the electrode surface. Table 3.2 provides values for the hydrogen reaction on different metals. Reactions with higher exchange-current densities occur more readily and result in higher current densities for a given overpotential. In contrast, reactions with very low exchange-current densities are slow or sluggish. The units on i_o are the same as those on i since the exponential terms must be unitless. The exchange-current density is also based on the same area as i. The exchange-current density includes the traditional chemical rate constant and concentration terms and is therefore a function of both temperature and concentration.

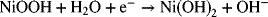
Table 3.2 i_o for Hydrogen Reaction in 1 m H₂SO₄ at 25 °C, values provide order of magnitude estimates

Metal	io [A·m−2]
Pb, Hg	10−8
Zn	10−7
Sn, Al, Be	10−6
Ni, Ag, Cu, Cd	10−3
Fe, Au, Mo	10−2
W, Co, Ta	10−1
Rh, Ir	2.5
Pd, Pt	10

The temperature dependence is exponential and can be represented by an Arrhenius expression. Values of i_o at different temperatures can be used to determine the activation energy needed to describe the temperature dependence. The dependence is described with

(3.18)

Here A is a constant and E_a is the activation energy in J·mol⁻¹ for the reaction.

The concentration dependence can be determined explicitly for the elementary reaction considered in the previous section as follows. First, the forward and reverse reactions in Equation 3.11 can be solved together for U to yield:

(3.19)

which is a form of the Nernst equation. This expression can be substituted back into either the forward or reverse rate expressions in Equation 3.11 to give

(3.20a)

Equation 3.20a applies to the single-electron elementary reaction that we have considered. In general, i_o varies with the surface concentrations of reacting species raised to a power. The concentration exponents can be determined from a mechanistic understanding of the reaction (see Equation 3.3) or by measuring i_o at different concentrations. Once the exponents are known, it is common practice to report i_o values as

(3.20b)

where the subscript ref refers to a reference concentration.

Finally, α_a and α_c are charge transfer coefficients and, as defined in Equation 3.17, have units of equiv mol⁻¹. These coefficients are positive and bounded (typically, α_a + α_c = n, the number of electrons transferred in the reaction of interest). Note that the terms αFη/RT must be unitless, and the units for R and T should be chosen accordingly. Information regarding the reaction mechanism can be inferred from experimentally measured values of α. For example, α_a = α_c = 0.5 indicates an elementary single-electron reaction.

ILLUSTRATION 3.2

The reaction

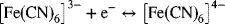
is sometimes used in analytical electrochemistry. This reaction can be assumed to be an elementary reaction. The exchange-current density for this reaction on a platinum electrode is 229 A·m⁻² and was measured at room temperature (25 °C) where both the reactant and product concentrations were 0.001 M. Experiments are being performed in a neutral 0.1 M KCl solution with a ferricyanide concentration of 0.02 M and a ferrocyanide concentration of 0.015 M.

1. Calculate the current that you would expect to measure from a 0.5 cm × 0.75 cm piece of platinum foil at a potential of 0.10 V versus a saturated calomel reference electrode (SCE). You may use simple activity corrections (neglect activity coefficients); liquid junction potentials may also be neglected. Please comment on the applicability of these assumptions.
2. A potentiostat is used to hold the potential of the Pt working electrode at the desired value versus the SCE reference electrode. What reaction do you think is being driven at the counter electrode?

SOLUTION:

1. First, we need the equilibrium potential for the reaction. A search online reveals that the standard potential for the reaction is 0.36 V. We will use Equation 2.25 to correct this value for concentration:This potential is relative to a SHE. We have assumed that the bulk concentrations given apply at the surface of the electrode. This assumption will not be good at high rates of reaction. Activity coefficient corrections should not be excessively large because of the relatively low concentration of ions. Also, the corrections to the numerator and denominator would be similar and tend to cancel. The liquid junction potential should be small since K⁺ and Cl⁻ have similar transport properties (remember that this correction is due to a potential created by unbalanced transport of the ions). Even so, we have undoubtedly included more significant figures than is warranted and will want to consider this in evaluating our final answer.In order to get the overpotential for the BV equation, the equilibrium potential and the electrode potential need to be relative to the same reference. 0.10 V SCE = 0.342 V SHE (you should verify this for yourself).The overpotential η_s is 0.342 − 0.3674 = −0.0254 V. The negative overpotential indicates that the cathodic reaction will dominate.We also need the exchange-current density at the concentrations of interest. From Equation 3.20, we getNote that the 0.5 values for the exponents are a result of the fact that we have a one-electron elementary reaction (see Equation 3.19). We can now plug the values into the BV equation to calculate the current density.The current density is negative since it is cathodic. To get the current, we must multiply by the area of the electrode. We assume that both sides of the electrode are active to give a total area of 0.75 cm². The resulting current from the electrode is therefore −0.306 A.
2. In order to set the potential of the Pt electrode at the given value, the potentiostat will drive an oxidation reaction at the opposite electrode. The easiest reaction to drive will be the oxidation of the ferrocyanide. If that reaction is not sufficiently rapid to provide the needed oxidation current, additional current will likely be provided by the oxidation of water to form O₂, a reaction that takes place frequently in aqueous electrochemical cells.

In summary, the Butler–Volmer equation was derived for a single-electron elementary reaction and then generalized. From a practical perspective, the BV equation is a three-parameter equation that can be fit to experimental data from a wide variety of electrochemical reactions.