Use of Kinetic Expressions in Full Cells

The purpose of this section is to help develop some initial experience and intuition with full electrochemical cells. By a full cell, we simply mean an electrochemical cell with the anode and cathode separated by some distance by an electrolyte. What’s more, we will consider the potential of the cell, namely, the potential of the positive electrode relative to the negative, rather than the potential of a single electrode relative to a reference electrode. The focus will still be on the rate expressions, although we will account for the potential drop in solution in a simple way in order to illustrate the influence of the potential field across the entire cell. Additionally, we will introduce some nomenclature that will be used extensively in future chapters on electrochemical cells. Concentration effects will not be treated in this section.

Let’s consider a system consisting of a Zn electrode and a NiOOH electrode in an alkaline solution. This is a galvanic cell where Zn will oxidize, and NiOOH will be reduced according to the following reactions characteristic of a Ni/Zn battery:

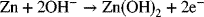
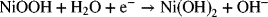
Given the geometric and physical property data in Table 3.3, we will find the following:

1. The difference in potential across the cell that corresponds to a current density of 1000 A·m⁻².
2. The discharge current that corresponds to a cell voltage of 1.3 V.
3. The charge current that corresponds to a cell voltage of 2.0 V.

Table 3.3 Parameters Used to Generate Figure 3.10

Symbol	Value	Explanation
Ra,Ni	100	Surface roughness factor for Ni electrode
Ra,Zn	2	Surface roughness factor for Zn electrode
io,Ni	0.61	Exchange-current density for Ni [A·m−2]
io,Zn	60	Exchange-current density for Zn [A·m−2]
T	298.15	Temperature [K]
UNi	1.74	Equilibrium potential of Ni relative to Zn reference electrode, V
αa,Ni	0.5	Anodic transfer coefficient for Ni electrode
αa,Zn	1.5	Anodic transfer coefficient for Zn electrode
αc,Ni	0.5	Cathodic transfer coefficient for Ni electrode
αc,Zn	0.5	Cathodic transfer coefficient for Zn electrode
κ	60	Conductivity of electrolyte [S · m−1]
L	2	Thickness of electrolyte (mm) (cell gap)

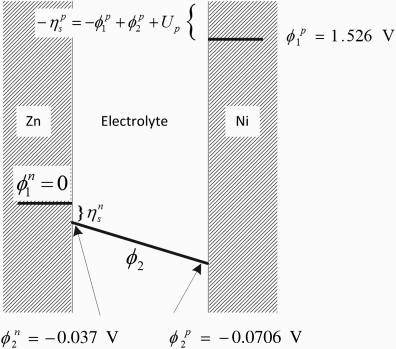
For our purposes here we will define the discharge current to be positive and the charge current to be negative. We treat the problem as one dimensional, with current flow between two flat electrodes of equal size and electrolyte in the gap L between the two electrodes. The potentials corresponding to 1000 A·m⁻² are shown in Figure 3.10 (left part). The zinc electrode is the negative electrode and the nickel is the positive one; these are designated with the superscripts n and p. There are three potentials that need to be considered: , the potential of the solution defined with respect to a reference electrode,  and , the metal potentials of the positive and negative electrodes, respectively. Note that  varies in the electrolyte between the two electrodes; therefore, the potential in solution at the zinc electrode is different than that at the nickel electrode.

The potential drop in solution obeys Ohm’s law, where

(3.36)

and κ is the conductivity of the electrolyte. The cell potential is the potential that you would measure if you connected the positive lead (usually the red wire) of your voltmeter to the nickel electrode and the negative lead (usually black) to the zinc electrode. This potential is defined as  and is always found as a difference rather than an absolute value. We may therefore arbitrarily designate a value for the potential at a point in the cell. In this one-dimensional problem, we specify the potential of the zinc metal to be zero, . We also specify  at the surface of the zinc electrode. In addition, we must choose a reference electrode for the solution. In this case, all potentials in solution are referred to a zinc reference electrode.

First, we find the potential of the cell that corresponds to a current density of 1000 A·m⁻². The potential V used in our kinetic expression is the potential of the metal relative to the potential of the solution just outside the double layer (see Equation 3.15b). Therefore,

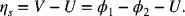
We will encounter a surface overpotential for both the negative and positive electrodes, and these values are different:

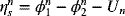
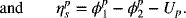
Since both the anode and the reference electrode are Zn, the equilibrium potential U_n = 0. When the current density i is known, we can move from one side of the cell to the other in steps as we solve for the potentials. We begin at the zinc electrode where the potential of the metal has been specified as . Writing the BV equation for the zinc electrode, the only unknown is the surface overpotential. Note that we have multiplied i_o,Zn by R_a,Zn in order to account for surface roughness that makes the actual area larger than the superficial area upon which the current density is based. Solving numerically yields . As expected, along the anodic branch, the overpotential is positive. This value is also , the potential in the solution at the surface of the zinc electrode just outside the double layer, because . Knowing the potential in solution at the zinc electrode interface, we can next calculate the potential drop in solution and hence the potential at the nickel−electrolyte interface.

(3.37)

Therefore, it follows that

(3.38)

Note that positive current flow is from the anode to the cathode and is accompanied by a drop in potential in the solution. The last step is to use the BV equation for the Ni electrode to calculate the potential of the solid phase,  for the Ni electrode. U_p is the equilibrium potential of the nickel electrode relative to a zinc reference electrode that is provided in Table 3.3. At 1000 A·m⁻², . On the cathodic branch, the overpotential is negative, and since the exchange-current density is smaller than for the zinc electrode, the magnitude of the overpotential is greater. Finally, we solve for the potential of the positive electrode, . The cell potential is  V. This is the potential that would be measured between the electrodes for the cell operating at the specified current density of 1000 A m⁻². These potentials are shown in Figure 3.10. Please study this figure carefully in order to help you understand how the potential varies in an electrochemical cell. Note that because the standard potentials of the two electrodes differ by almost 2 V, this figure is not to scale.

Next, in the right part of the figure, we find the discharge current that corresponds to a cell voltage of 1.3 V. Since the cell voltage is  and we can specify the absolute value of the potential at one point, we arbitrarily set . It follows that . Solution of this problem is a little more complicated when the current density is not known. In this case, we must solve the problem iteratively. The problem can be solved by manual iteration, guessing a current density, calculating a cell potential, and adjusting our guess until the calculated cell voltage matches the specified value. It is much more efficient to simultaneously solve three equations for the three unknowns numerically.

Note that the current density in solution is defined as positive when moving from anode to cathode. In contrast, the cathodic current density, which flows in the same direction, is defined as negative by convention. Hence, the current in solution must be set equal to the negative of the cathodic current.

This procedure works equally well for charge as for discharge without the need to modify the equations. However, for charging, the specified potential between the electrodes must be greater than the open-circuit voltage. Thus, solving the same set of equations for an applied potential of 2.0 V yields a charging current of −821 A·m⁻².

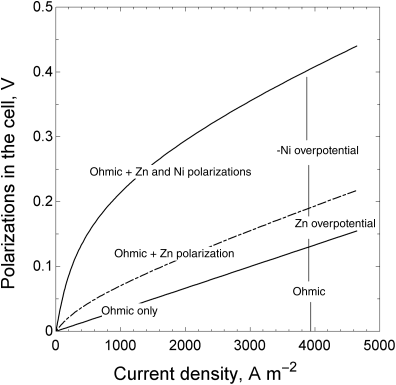
The total voltage loss, or polarization, across the cell is equal to . The model that we have developed can be used to evaluate the relative magnitude of each of these losses as a function of current, as shown in Figure 3.11. Examination of the figure shows that the overpotential at the zinc electrode is much less than that at the nickel electrode. Note also that the potential drop in solution increases linearly with current in the absence of concentration gradients, and that its relative importance is greater at the higher currents.

One final note, the reference electrode described here is unlikely to be physically “just outside the double layer.” Recall, the typical double layer is only a few nanometers thick. In fact, the reference electrode may be far removed from the electrode surface. As a result, there will be a difference in the potential that is measured by this reference electrode and what is needed for the kinetic expression. Placement of the reference electrode and correcting for this difference in potential will be covered in subsequent chapters. For our purposes here, when the overpotential is reported, assume that the correction has been made so that the potential corresponds to one measured by a reference electrode that is just outside the double layer, even if it is hypothetical. In some of the problems at the end of the chapter on full cells, you may be told that the ohmic resistance has been removed or you may need to subtract it to focus on the kinetic polarization.