In Equation 4.3, both the ion mobility and a diffusion coefficient appear. Both the concentration and the potential impact the electrochemical potential (μ_i). While the details are beyond the scope of this text, it is the gradient of the electrochemical potential that is the true driving force for transport. Therefore, we might expect the diffusivity and mobility to be related. That relationship is

(4.27)

which is the Nernst–Einstein relationship for dilute solutions. This equation provides us with a convenient way of estimating one of these parameters from knowledge of the other.

Now let’s take a second look at the Nernst–Planck equation in the absence of concentration gradients:

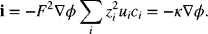
We see that the total current is the sum of contributions from movement of the individual species. This observation leads to the definition of a second convenient transport property, the transference number,

(4.28)

The quantity can be thought of as the fraction of current carried by species i in the absence of a concentration gradient. Similar to Ohm’s law, it has this intuitive physical meaning only when the concentration is uniform; nonetheless, the transference number represents a key transport property of the electrolyte. From its definition, it can be seen that the sum of the transference numbers for the individual ions is unity,

(4.29)

ILLUSTRATION 4.3

Calculate the transference number of the ions present in an electrolyte that is 0.5 M CuSO₄ and 0.1 M H₂SO₄. Assume complete dissociation of the ionic species.

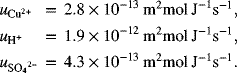
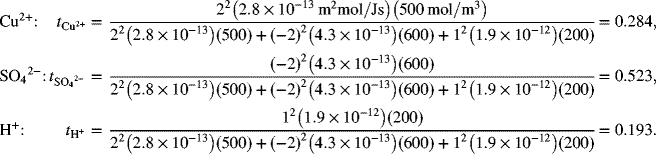
Note that even though the mobility of the hydrogen ion is much higher, the majority of the current is carried by the sulfate ion because of its higher concentration, higher charge per ion than H⁺, and a mobility that is greater than that of the cupric ion.

If a current density of 1000 A·m⁻² is applied and current is positive when it flows from left to right in the system, what is the magnitude of the migration flux (mol·m⁻²·s⁻¹) for each of the ions, and in which direction do the ions move? Assume that the concentration is constant.

In the absence of concentration gradients, all current flow is due to migration. Under these conditions (e.g., at short times before concentration gradients develop or when convection is sufficient to keep the concentrations constant), we can relate the flux of individual species to the portion of the current that is carried by that species:

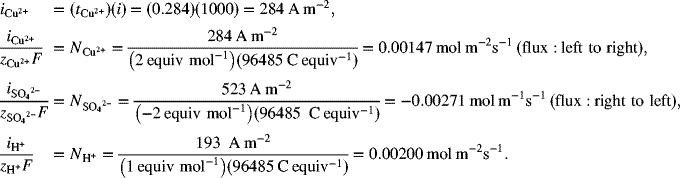
Remember, this calculation is valid only for systems without concentration gradients. It is interesting to see that the flux of the hydrogen ion is higher than that of copper, but it still does not carry as much current. The equivalent ionic conductance is often reported in the literature rather than the mobility (u_i) or diffusivity (D_i) of individual ions. The symbol for the equivalent ionic conductance is λ_i, with units of S·cm²·equiv⁻¹. Thus, λ_i is the conductance per equivalent. Ionic conductance is related to the mobility as follows:

(4.30)

The values for λ_i will depend on the solvent, the species, the temperature, and the concentration. However, one typically finds values tabulated for common ions in water at room temperature at infinite dilution. There are theories that attempt to predict the dependence on concentration, for example; but, for the most part, these transport properties must be measured for practical electrochemical systems. Here we will only look at a simple salt that dissociates into one anion and one cation of equal charge. The conductance is given by the sum of the conductance of the two ions.

(4.31)

Cation	Equivalent conductance, λi [S·cm2·equiv−1]	Anion	Equivalent conductance, λi [S·cm2·equiv−1]
H+	349.8	OH−	197.6
Li+	38.69	Cl−	76.34
Zn2+	53	HSO4−	50
Na+	50.11	SO42−	80
Cu2+	54	Br−	78.3
K+	73.52	NO3−	71.44

ILLUSTRATION 4.4

Calculate the (a) conductivity, (b) transference number of Na⁺, and (c) diffusivity of 0.1 M NaCl from values for equivalent conductance.

1. The concentration is 0.1 M, which is equal to 0.1/1000 equiv cm⁻³. Substituting into Equation 4.31 gives κ = 0.01265 S cm⁻¹. The experimental value is 0.01067.
2. Using Equations 4.28 and 4.30, the transference number of the sodium ion is simply
3. The diffusion coefficient of the salt is given by Equation 4.20:

Binary Electrolyte: Lithium-Ion Battery

Now that we have examined transport properties, let’s consider an additional example that involves a binary electrolyte. Specifically, let’s look at transport in the separator of a lithium-ion battery. The electrolyte consists of an organic solvent into which a salt of lithium is dissolved (e.g., LiPF₆). The salt is assumed to dissociate completely to form a binary 1:1 electrolyte. For simplicity, we will treat the electrodes as planar even though porous electrodes are used in practice (see Chapter 5). During charging of the battery, lithium ions are reduced at the negative (left electrode) and lithium oxidized at the positive electrode (right side). The anion does not react at either electrode. Thus, in effect, we are shuttling lithium ions from one electrode to the other. Graphite is a typical negative electrode, and metal oxides are commonly used for the positive electrode. The half-cell reactions of interest are

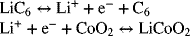
Convection is neglected. We can write the flux of cations and anions using the Nernst–Planck equation for one-dimensional transport in the x-direction as

(4.32)

(4.33)

Since only lithium ions can react, these are the only ions responsible for current, which can be expressed as

(4.34)

For the anion, however, the flux must be equal to zero. Thus, we can use Equation 4.33 to express the potential gradient in terms of a concentration gradient.

(4.35)

This expression can be substituted back into Equation 4.32 to eliminate the potential. Also note that although the concentration of the salt will change, because of electroneutrality, c₋ = c₊ = c since ν₊ = ν₋ = 1. Thus,

(4.36)

If we now introduce the following for the transference number and the diffusivity of the salt:

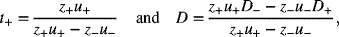
we arrive at

(4.37)

Equation 4.37 can be generalized rather simply by adding ν₊ so that it applies to any binary electrolyte where only the cation reacts, a situation that is quite common. The general expression is

(4.38)

where the simplification in the middle expression was obtained via the Nernst–Einstein relation.

Now that we have the needed expression for the flux as a function of the salt concentration, we can move forward to solve for the concentration profile in the lithium-ion battery containing a binary salt. As we saw earlier, for a binary electrolyte, the equation for convective diffusion applies. Neglecting convection, the material balance for the salt is .

A battery is inherently a transient device whose state-of-charge changes continuously during charge and discharge (see Chapter 7). However, batteries are often operated at conditions where the time required for the transport processes to reach steady state, as characterized by the diffusion time (L²/D), is short relative to the time scale that characterizes the chemical conversion. Physically this means that the concentration gradient changes relatively quickly compared to time it takes to charge or discharge the battery. Under such conditions, a pseudo steady-state is maintained. Consequently, if we assume steady-state for a one-dimensional case with constant diffusivity, we are left with Laplace’s equation for the concentration, which we can integrate to show that the concentration varies linearly with position,

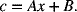
We can now use Equation 4.37 to find the constant A. Also, since the electrolyte is not involved in the reactions, lithium ions are simply shuttled between electrodes, the amount of salt is constant. This conservation of lithium allows for the evaluation of the second constant B. The net result is

(4.39)

Figure 4.7 shows the concentration graphically for discharge (i is positive). Since the amount of salt is fixed, the average concentration cannot change. Therefore, the concentration is constant in the middle of the separator. As the current density increases, two undesired results are possible. The concentration of the salt and therefore lithium can go to zero at the electrode surface (x = 0). This case represents a limiting-current behavior. A second possibility is seen at the opposite electrode where the concentration increases with current density. There is the risk of exceeding solubility limits at that electrode, which would lead to salt precipitation.

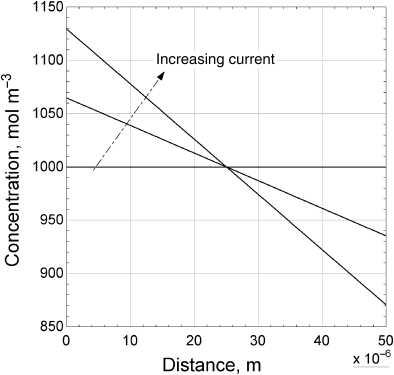
The impact of the transference number for the lithium ions can be seen in Equation 4.39. An increase in the transference number for the lithium ion leads to a lower concentration gradient for a particular flux (or current). As the transference number approaches one, the concentration gradient of the salt goes to zero. In general, it is desirable to have a high lithium-ion transference number in these batteries.

ILLUSTRATION 4.5

Calculate the following quantities given data for conductivity and transference number of an electrolyte in a separator of thickness 200 μm. The initial concentration of the salt is 800 mol m⁻³. Also, κ = 1.3 S m⁻¹ and t₊ = 0.4.

1. Diffusion time. The conductivity and transference number can be expressed in terms of mobilities (Equations 4.7 and 4.28). Solving for the mobilities givesThe time for diffusion is  , which is short relative to the time typically required to charge or discharge a battery.
2. Limiting current, corresponding to zero concentration at the electrode surface at x = L, is given by
3. Potential drop at half of limiting current measured instantly after the start of the current flow. Before there is time for the concentration gradient to develop, the potential drop will be given by Ohm’s law.
4. Once sufficient time elapses, a concentration gradient will develop and the modified form of Ohm’s law is used, Equation 4.5, which is integrated to giveThus, as the concentration gradient develops, the potential drop decreases by about 5 mV.