For convenience, values of standard potentials have been determined and tabulated for a large number of electrochemical reactions, a subset of which is found in Appendix A. Although listed as half-cell reactions, the potentials represent the difference between the potential of the reaction of interest and a reference reaction. The universal reference is the standard hydrogen electrode (SHE). Hence, the standard potential for the hydrogen reaction is defined to be zero. Tables of standard potentials are typically written as cathodic (reduction) reactions. Be mindful that for our thermodynamic analysis these reactions are assumed to be in equilibrium. Reactions whose standard potentials are positive relative to hydrogen naturally act as cathodes when coupled with hydrogen. In contrast, reactions with negative potentials are more anodic than hydrogen. A table such as that found in Appendix A is also a good place to start when you are unsure of how a particular compound might react. For example, the number of electrons transferred and the products produced can be readily determined from the table for a variety of elements.
The standard potential for the overall reaction can be obtained from the standard potentials of the two half-cell reactions (each relative to SHE) as follows:
where the “right” and “left” refer to the cell diagram similar to that illustrated in Figure 2.1b. Since the values of 
for the two half-cell reactions are both relative to hydrogen, the influence of the reference subtracts out, and we are left with the desired quantity.
ILLUSTRATION 2.1
Let’s determine the standard potential for the Daniell cell shown in Figure 2.1. We see that the standard potential of the Cu is above that of the Zn reaction in Appendix A. Thus, the Cu electrode is shown on the right in the analysis diagram. The full-cell reaction is
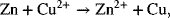
where n = 2. The standard potential is
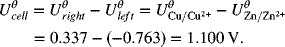
Let’s consider a second example where the negative reaction is still the Zn reaction, but the positive reaction is replaced by the oxygen reaction on the right side: 
.
The full-cell reaction is 
, where n = 4.
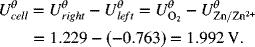
Note that in the second example shown in the illustration it was necessary to multiply the stoichiometry of the negative reaction by two in order to get the electrons to balance and yield the correct overall reaction. However, we did not multiply the standard potential by the same factor. This practice may seem counterintuitive, but is correct. The standard potential represents the energy per charge, which does not change when you multiply the equation by the factor needed to make the electrons balance. The Gibbs energy changes because more electrons are involved, but the value per charge remains the same. This invariability will persist as long as the ratio of the number of electrons per mole(s) of reacting species remains the same. In other words, it doesn’t matter if you have 2 electrons per mole of zinc, 4 electrons per 2 mol of zinc, or 5000 electrons per 2500 mol of zinc; the energy per unit charge is the same. That ratio always remains constant for the situation that we have considered involving a balanced anodic and cathodic reaction. Reworking the problem above with use of 
helps illustrate the point:
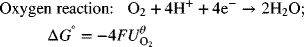
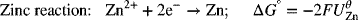
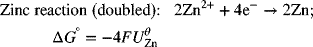
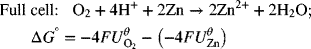
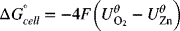
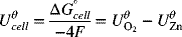
As you can see, the total number of electrons for the anodic and cathodic reactions is the same, which results in 
equal to the difference between that of the two half-cell values (Equation 2.12).
In the above example, it appears that we used Equation 2.3 to describe 
of the half-cell reactions. However, as apparent from its derivation, Equation 2.3 only applies to full-cell reactions where the electrons are balanced; this equation relates the Gibbs energy change of the chemical species to the electrical work resulting from the difference in the electron energies that correspond to each of the half-cell reactions at equilibrium. Implicit in the use of Equation 2.3 for a “half-cell” is the fact that the other half is the standard hydrogen electrode, whose Gibbs energy is, by definition, equal to zero. The hydrogen portion simply subtracts out when we calculate 
as shown above. Subtracting off a balanced full-cell reaction does indeed reverse the sign of its 
as shown in the example. In contrast to the above, calculation of the Gibbs energy change for the half-cell alone must involve the chemical potential of the electrons as demonstrated in Section 2.12.
Half-Cell Potentials Not in Table
What do we do if the reaction that we need is not in the table of standard potentials? One possibility is to combine existing half-cell reactions to create the desired half-cell reaction. In doing so, we always go through the Gibbs energy route (just demonstrated above) in order to avoid errors. The creation of a new half-cell reaction will of necessity not balance electrons since we want electrons in the final expression.
To illustrate:
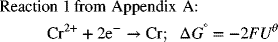
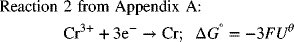
To get the desired reaction, we subtract Reaction 1 from Reaction 2:
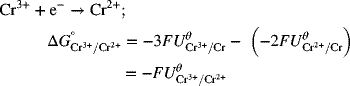
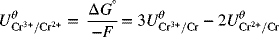
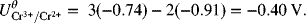
As you can see, the standard potential for the new half-cell reaction is not just the difference between half-cell potentials of the reactions that were combined. The reason for this adjustment is that the Gibbs energies above actually correspond to full-cell values with hydrogen on the left as the anode. In cases where we have electrons left over, the hydrogen reaction does not cancel out as it does when the electrons balance, and we are left with the difference between the half-cell of interest and the hydrogen electrode, consistent with other standard potentials. Consequently, it is important to use Gibbs energies when combining half-cell reactions to form a new half-cell reaction.
Standard Potential from Thermodynamic Data
Standard potentials for the cell can also be calculated directly from Gibbs energy data using Equation 2.3. The standard Gibbs energy of formation is tabulated for compounds in different states (gas, liquid, aqueous, and solid) assuming they are formed from the elements taken at 25 °C, 1 bar pressure. For a cell reaction,
where si are the stoichiometric coefficients for the reactants and products. By convention, si is positive for products and negative for reactants. As we have seen above, reactants and products of electrochemical reactions usually include ions. Because of the definition of the standard state for ions in electrolyte systems, which includes only interactions between the solvent and the ion of interest, the standard state Gibbs energy does not depend on the counterion(s) in the system. Rather, the impact of the counterions is included in the activity term. Therefore, tabulated values of 
for the ions involved in the reaction should be used where available (see Appendix C), and are frequently tabulated for aqueous systems. When single-ion values are not available, the difference in the Gibbs energy of formation for ionic species can be calculated from 
for two neutral aqueous (aq) species with the same counterion. For the dissociation of a neutral species,
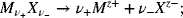
and from Equation 2.13
(2.14)
Therefore, the counterion portion will cancel out when the aqueous values are subtracted (see Illustration 2.2). Finally, a combination of 
and S° data can be used to estimate 
. The following illustration demonstrates how to determine 
for each of the situations mentioned above.
ILLUSTRATION 2.2
The balanced reaction for the oxidation of Fe by oxygen is
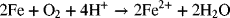
where four electrons are transferred in the reaction. We have already used half-cell potentials to calculate the standard potential. We will now calculate the potential from Gibbs energy data (ions and neutral species), and from enthalpy and entropy data. Note that the calculation below is for the reaction as written, specifically for 1 mol of oxygen.
- Gibbs energy data using ionic species:
for liquid water- From Equation 2.13,
- Therefore,
- Gibbs energy data using neutral aqueous species:
which is the same value as above. Note also that the difference between the iron chloride and the hydrogen chloride terms yielded the same value as obtained from the Gibbs energies of formation for the ionic species since the chloride contribution cancels out.
- Enthalpy and entropy data:
Leave a Reply