Tafel Approximation

The BV equation has two exponential terms, one that represents the anodic current (i > 0, η_s > 0) and the other that represents the cathodic current (i < 0, η_s < 0). What happens to the relative magnitude of the two terms as η_s becomes more positive? What about as η_s becomes more negative?

When η_s is large and positive, the anodic term of the BV equation dominates and the cathodic term does not contribute significantly to the current. Basically, the activation energy changes as a function of the potential until that corresponding to the cathodic reaction becomes much larger than that for the anodic reaction. Under such conditions,

(3.23)

This simplified expression is called the Tafel equation. It can be readily solved for the overpotential as a function of the current:

(3.24)

Equation 3.24 is the equation of a line for η_s versus ln i. Both α_a and i_o can be determined from experimental current–voltage data by fitting a line to the data. One of the advantages of the Tafel equation is that there is one less parameter to fit (two rather than three). In the past, when most analysis was done graphically, it was common practice to use the base₁₀ logarithm in analysis rather than the natural logarithm. We also use base₁₀ logarithms in log–log and semi-log plots because such plots are easier to read. Equation 3.24 can be written accordingly as follows:

(3.25)

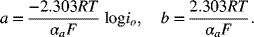
This equation yields a slope of 59.2 mV per decade for an α_a of 1. The slope of experimental data can be used as a quick reference for determining α. For example, a Tafel slope of about 118 mV per decade would correspond to a single-electron reaction with α_a equal to 0.5. Note that a decade is one x unit on the base₁₀ semi-log plot of η_s versus log i.

A similar development can be used to obtain a Tafel expression for the cathodic reaction at large negative values of η_s:

(3.26)

(3.27)

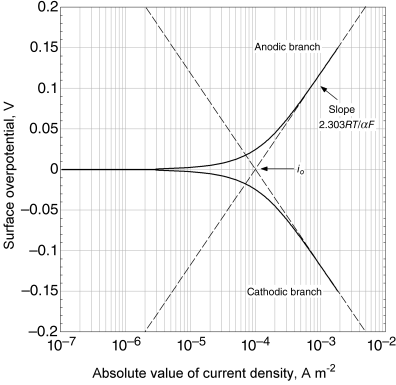
Note that i < 0 for cathodic current so that −i is positive as it must be inside the logarithm. To emphasize this, we have included the absolute value in the last term of Equation 3.27 and on graphical representations of the equation. The slope of the cathodic curve is negative. A classical Tafel plot is shown in Figure 3.7 for η_s as a function of log |i|. Both the anodic and cathodic Tafel lines have been included, which meet at η_s = 0, where . The absolute value of the current from the full BV equation is also shown. The Tafel approximation and the full BV equation are identical at high overpotentials, but diverge as the overpotential approaches zero. As mentioned above, such plots are useful for fitting parameters to experimental data. These types of plots have also been used extensively to analyze corrosion systems (see Chapter 16), among others.

How large must the overpotential be in order for the Tafel expression to be valid? To address this question, we compare the current from the Tafel expression with that from the corresponding full BV equation. That comparison yields the following:

(3.28)

where B is a constant that is equal to 0.12 V for a maximum error less than 1%, and 0.062 V for a maximum error <10%. Equation 3.28 provides an easy way to determine the minimum value of the overpotential that meets these error specifications. However, it assumes that α_a and α_c are known. This, of course, does not help if you are using the Tafel expression to fit data in order to estimate these parameters. A general rule of thumb is that the overpotential should be greater than about 100 mV for use of the Tafel simplification. Graphical examination of the data that you are fitting will also allow identification of the linear region (semi-log plot) that can be used for parameter fitting with the Tafel equation.

ILLUSTRATION 3.3

Kinetic data are provided for the evolution of chlorine in 5 M NaCl at 20 °C (J. Electrochem. Soc., 120, 231 (1973)). a) Write the reaction for the evolution of chlorine. Is this anodic or cathodic? b) What is the Tafel slope for the reaction? c) Determine the exchange-current density for this reaction. d) Find the transfer coefficient α_a.

Current density [A·m−2]	Overpotential [V]
60,300	0.2091
41,300	0.1994
22,300	0.1703
12,400	0.1515
8,080	0.1359
6,180	0.1208
4,110	0.1036
2,070	0.07934
1,230	0.05512
817	0.04727
621	0.04047
427	0.03433
240	0.02547
173	0.02204
116	0.01658
58.4	0.01175
30.1	0.00489

1. The reaction isBecause electrons are released, this is an anodic reaction.
2. According to the Tafel equation, the current density isTaking the logarithmand rearranging results, an equation of the form y = ax + b,The overpotential data are plotted as a function of the logarithm base 10 of the current density. As expected, the relationship is not linear over the entire range. At larger overpotentials, the Tafel equation should apply and the slope is constant. A line is fitted through the data points at overpotentials greater than 50 mV. The slope of the fitted curve is 92 mV per decade.
3. The Tafel equation reduces to i = i_o when the overpotential is zero. Graphically, the fit is extrapolated to η_s = 0, and the value for the exchange-current density is read off the graph. Alternatively, the value is calculated from the regression fit:Solving, i_o = 292 A·m⁻².
4. Using the slope fitted to the data,Thus,

Linear Approximation

The BV equation can also be approximated at low overpotentials by expanding the full BV expression in a Taylor series around η_s = 0, and keeping the first two terms of the series for both the anodic and cathodic portions:

(3.29)

(3.30)

The resulting linear expression is accurate for small values of η_s and is typically used when the overpotential is 10 mV or less. The error associated with use of this approximation varies with the parameters used.