Now that we have a way of obtaining  for use in Equation 2.11, we must add the activity correction to get the desired expression for U. A discussion of activities and standard states for electrolytes is provided later in Section 2.14. Activity is a dimensionless quantity that depends on the standard state for each species. As a first approximation, we simply use the following:

(2.21a)

(2.21b)

(2.21c)

(2.21d)

The standard state for gaseous species is an ideal gas at 1 bar, and for ions in solution it is an ideal 1 molal solution. As a first approximation, we will use concentration as a proxy for molality. With these assumptions, Equation 2.11 becomes

(2.22)

where s_i is positive for products and negative for reactants. This equation is similar to the classical Nernst equation. The assumptions implicit therein are those most frequently used to approximate cell potential. Note that because of our assumption of unit activity for any solid reactants and the solvent, these species do not appear in Equation 2.22. The following illustration demonstrates the use of this equation and the process developed above to calculate the cell potential.

ILLUSTRATION 2.4

For the chlor-alkali cell described in Illustration 2.3, please determine the equilibrium potential at 25 °C and 2 bar (each side is at this pressure).

As usual, we write the half-cell reactions with the positive electrode on the right side (see Figure 2.1b).

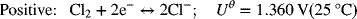
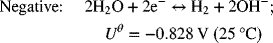
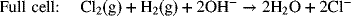
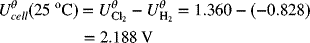
The full-cell reaction is written in the spontaneous direction, which gives a negative change in Gibbs energy and a positive potential. The number of electrons in the balanced reaction is 2, with products on the right. The OH⁻ concentration of interest is that on the alkali side. This is important since the hydroxide concentration is different on the two sides of the cell. pH = 14; 

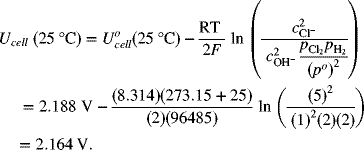
Our approach to calculating the cell potential in the above illustration, consistent with the discussion in the chapter to this point, has been the following:

1. Write down the two half-cell reactions of interest and the standard potential for each reaction.
2. Put the reaction with the most positive standard potential on right side of the electrochemical cell as the cathode. The other reaction is the anodic reaction.
3. Write the full-cell reaction that appropriately combines the cathodic and anodic reactions. Make sure that the electrons are balanced.
4. Take the difference between the two standard half-cell potentials to get the standard potential for the full cell (cathode potential – anode potential).
5. Use the simplified activity corrections to correct the cell potential with the products on the top and the reactants on the bottom. Use the full-cell reaction to get the stoichiometric coefficient for each species and the total number of electrons for the reaction.

In using this approach, it is necessary to keep track of the location of the reactant and product species in order to make the required activity corrections, since those corrections, of necessity, use the environment adjacent to the electrode of interest. For example, in Illustration 2.4, the pH on the anodic side of the cell is approximately 4, and that on the cathodic side is about 14. Therefore, we have two different pH values that might be used to make the activity correction. In the example, we correctly selected a pH of 14 since the cathodic reaction depends on pH, whereas the anodic reaction does not. In other words, the activity corrections require us to use the concentration(s) that applies locally to each half cell. An alternative approach to finding the cell potential that many students find easier to use is to first determine the potential of each half cell relative to the SHE, including activity corrections, and then take the difference between the two half-cell potentials to get the full-cell potential. This approach is analogous to that used to calculate the standard potential, but has been expanded to include the needed activity corrections. The potential of any reaction versus SHE can be found from the following equation:

(2.23)

where all of the activity corrections belong to the half-cell reaction of interest since there are no activity corrections, by definition, for the SHE. Note also that  and that the half-cell reaction was assumed to be expressed as

(1.10)

For half-cell reactions that are of the simple form

(2.24)

U can be written as

(2.25)

where we have kept the standard potential for hydrogen in the equation to emphasize the fact that this potential is relative to SHE. This equation assumes that both the oxidized and reduced species are ions in solution, where the oxidized form of A is on the same side as the electrons in Equation 2.24. The reference concentrations were not explicitly included for the purpose of simplification since they are equal to unity. The following illustration demonstrates the alternative approach to calculating the full-cell potential.

ILLUSTRATION 2.5

For the chlor-alkali cell described in Illustration 2.3, please determine the equilibrium potential at 25 °C and 2 bar (each side is at this pressure).

As usual, we write the half-cell reactions with the positive electrode on the right side (see Figure 2.1b). However, we will now correct each electrode separately for activity effects.

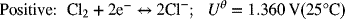
Correcting this electrode for composition gives the half-cell potential relative to SHE:

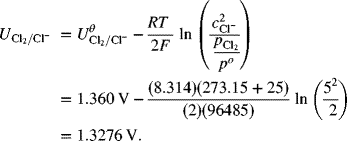
Now repeat this same procedure for the negative electrode.

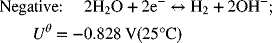
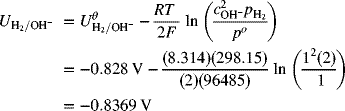
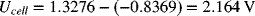
This value is the same answer as above. However, there was no need to write and balance the full-cell reaction, and there was no confusion regarding which concentration to use (that adjacent to the half-cell of interest). As a reminder, the spontaneous direction is where the more positive electrode is the cathode.

In these illustrations, the activity correction was small relative to the equilibrium voltage determined under standard conditions. While this is often the case, there are situations where the corrections make a significant difference and change the conclusions that would otherwise be made.