We will find the Butler–Volmer formulation of kinetics extraordinarily useful for the study of electrochemical systems. Nonetheless, it is largely a phenomenological or empirical equation with three parameters, io and two transfer coefficients, αa and αc. We saw vast variations in exchange-current densities based on the reactions and the electrode surface. What causes one reaction to be facile and others to be sluggish? The answer to these questions must be rooted in the chemical environment of the reactants and products as well as the structure of the interface between the electrode and the electrolyte. These fundamental studies have been pursued extensively, and in fact two Nobel Prizes for Chemistry have been awarded in the field of electron transfer reactions in chemical systems (Henry Taube, 1983 and Rudy Marcus, 1992). Although the theory is still far from complete, it is instructive to consider a few aspects and results from these works.
First, we should like to distinguish between two types of electron transfer reactions: inner sphere and outer sphere. For outer sphere reactions, the reactants and products do not interact with the electrode surface. Rather than being adsorbed onto the surface, they may be a solvent layer away from the surface. You might expect that for these types of reactions, the nature of the electrode surface is less important. In contrast, inner sphere reactions have strong interactions with the electrode surface and often involve specific adsorption. The oxygen and hydrogen reactions are two examples of inner sphere reactions. As we saw from Table 3.2, the electrode material plays a critical role in determining the exchange-current density. As a specific example, this dependence may be explained in part by understanding the mechanism of the hydrogen reaction in more detail. We can view the metal surface as a collection of possible sites for adsorption of hydrogen. The hydrogen reaction proceeds through two steps, referred to as the Volmer−Tafel mechanism. Dissociative adsorption of molecular hydrogen onto two metal sites, S, takes place first, and is followed by the electron transfer reaction.


The adsorption step is relatively slow and thus rate determining. If hydrogen adsorbs either too weakly or too strongly, the reaction is inhibited. First principles calculations of the strength of adsorption on different metals predict the trends in exchange-current density with different materials.
Reaction theory is most developed for the so-called outer sphere reactions. These reactions are more tractable because the interactions with the electrode surface are absent. Let’s compare a reaction already encountered in this chapter and treated with the phenomenological Butler–Volmer equation to an isotope exchange reaction:
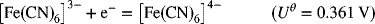
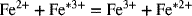
The first is the ferri/ferrocyanide reaction and the second is the reaction between Fe(II) and Fe(III). The asterisk refers to an isotope of iron, and this reaction is an isotope exchange reaction. In both cases, no chemical bonds are broken or formed. In contrast to what might be intuitive, the ferri/ferrocyanide reaction is relatively fast compared to the isotope exchange reaction. This result can be understood in terms of the reorganization energy, λre (not to be confused with the Debye length, which also uses λ). There are two components of this reorganizational energy representing solvation and vibrational energy terms. When, because of electron transfer, the charge of the species changes, its chemical environment must adjust to the new equilibrium. The theory predicts that the change in Gibbs energy of the activated complex is proportional to this reorganizational energy:
(3.21)![]()
Thus, the larger the reorganization energy, the smaller the rate constant. For the bulkier ferricyanide complex, the change in charge has a relatively smaller effect and the reorganization needed is much smaller, and therefore the reaction is faster.
A second key result from the theory has to do with the transfer coefficient:
(3.22)![]()
Here we note that generally the term involving the reorganizational energy λre is small, and therefore a transfer coefficient of 0.5 for an elementary single-electron transfer reaction has some theoretical basis. Furthermore, we see that there is no dependence of the transfer coefficient on temperature, but a small dependence on potential. It is also important to note that Equation 3.22 is for outer sphere reactions. For inner sphere reactions, the interactions with the electrode must be considered, and one can neither expect the transfer coefficient to be 0.5 nor to be independent of temperature and potential.
Leave a Reply