Electrochemical reactions take place at the surface of the electrode as electrons are transferred to and from ions or neutral species in solution. The rate of reaction is influenced by the potential drop across the double layer. At open circuit (no external current), this potential drop reaches an equilibrium value where the forward and reverse reactions are equal. One of the real advantages of electrochemical reactions is that the rate of reaction can be controlled by changing the potential of the metal, which changes the potential drop across the double layer and, therefore, the rate of reaction across the interface. By changing the potential of the metal, we can control the rate and even the direction of the reaction. The main purpose of this chapter is to develop a relationship between the rate, expressed as a current density, and the potential, and to illustrate how this relationship can be used.

The reference point for our discussion of reaction rate is the equilibrium potential where the net rate of reaction is zero. What happens when we increase the potential or, in other words, make the potential more positive than the equilibrium potential? Increasing the potential lowers the energy of electrons in the electrode (remember, electrons are negatively charged) and makes it easier for molecules or atoms to lose electrons to the electrode. Thus, values of the potential that are positive relative to the equilibrium potential promote the anodic reaction (oxidation). As you may have guessed, the opposite is true for potentials lower than the equilibrium potential. Lowering the potential increases the energy of electrons in the electrode and promotes the transfer of electrons from the electrode to, for example, a species in solution (reduction). Therefore, the cathodic reaction is favored as the potential is lowered relative to the equilibrium potential. The situation is summarized in Figure 3.3 using the reaction of ferric (Fe³⁺) and ferrous (Fe²⁺) ions as an example.

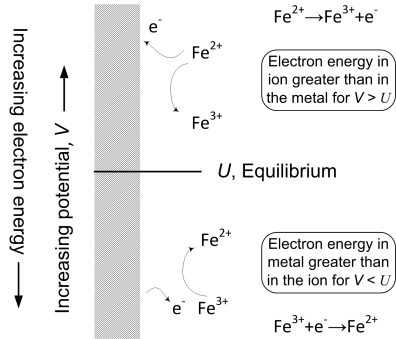
There is one slight problem. The potential difference (ϕ_m − ϕ_s) between the metal and the solution just outside the double layer (see Figure 3.2) cannot be measured directly. The reason for this is easy to understand. Potentials are measured between two electrodes. However, if we put another electrode into solution to measure ϕ_s, it will also form its own double layer with its own potential drop. Therefore, what you end up measuring is a combination of the potential drop associated with the two electrodes. Fortunately, this problem is easy to overcome, as mentioned in Chapter 2. We simply express all potentials relative to a reference electrode, which defines our potential scale. Thus, what you learned about reference electrodes and potential in the previous chapter provides the needed reference point for our discussion of kinetics.

ILLUSTRATION 3.1

You have been given a solution containing Fe³⁺ and Fe²⁺ ions at a pH of 3. Two inert Pt electrodes are placed into the beaker and one of the electrodes is set at a potential of 0.44 V versus SHE. Will ferrous ions be oxidized or will ferric ions be reduced at that electrode? Is there any chance of depositing metallic iron on the electrode? Your lab partner claims that at 0.44 V you will also evolve hydrogen. Is she correct?

SOLUTION:

The reactions of interest are as follows:

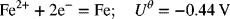
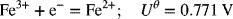
where the standard potentials have been provided. Since no concentration information was given in the problem statement, and corrections for concentration are typically small relative to the standard potential, we will make our assessment with use of the uncorrected potentials.

We are asked to assess whether ferrous  ions will be oxidized or ferric  ions will be reduced at an applied potential of 0.44 V versus SHE. The relevant equilibrium potential is that of the second reaction, 0.771 V. Since the applied potential is lower than the equilibrium value, the reduction reaction takes place. Therefore, ferric ions are reduced. Incidentally, this would mean that this electrode is the cathode.

Will iron deposition occur? The applied potential of 0.44 V is well above the equilibrium potential of −0.44 V. Therefore, iron will not deposit on the Pt electrode.

Will hydrogen be evolved at the electrode? The applied potential of 0.44 V is also above the equilibrium value for hydrogen (0 V). Therefore, hydrogen will not be evolved.

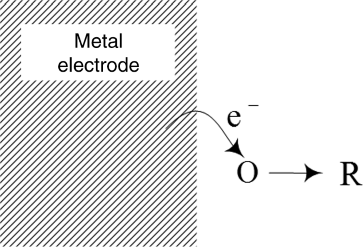
Having examined qualitatively how the potential affects the direction of the current in the last section, we now seek a quantitative expression for the current density as a function of potential. To do this, we consider a single-electron elementary redox reaction (also see Figure 3.4):

(3.3)

where O is the oxidized species and R is the reduced species. As already discussed, both the forward (in this case, reduction) and reverse reactions take place simultaneously on the same surface. At the equilibrium potential, the net rate of reaction is zero, whereas the anodic reaction dominates at potentials positive of U, and the cathodic reaction dominates at potentials negative of U. By convention, we define anodic current to be positive.

Similar to chemical reactions that you may have studied previously in a chemistry class, there is an activation energy associated with both the forward and reverse reactions as shown in Figure 3.5. To react, an energy barrier must be overcome to reach a transition state (i.e., activated complex), whose energy corresponds to that at the top of the energy curve. This activation energy is a function of temperature, as taught in a beginning chemistry course. The rate of the forward reaction can be written in terms of the reactant concentration and a rate constant, k_f, that is a function of , the Gibbs energy difference between the initial reactants and the transition state. Assuming a first-order elementary reaction (see Equation 3.3),

(3.4)

where c_O is the concentration of the oxidized species. A decrease in  corresponds to a lower activation energy and will cause the rate of the forward reaction to increase. A similar expression can be written for the reverse reaction. The same type of model applies to electrochemical reactions, with one important difference.

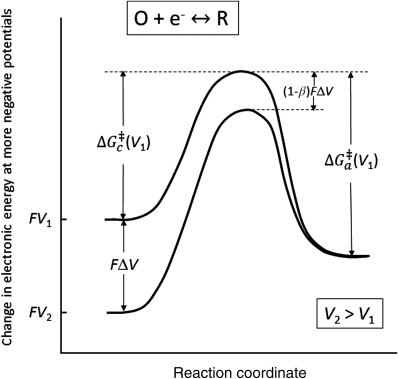
We can modify the activation energy of electrochemical reactions by changing the electrode potential, as shown in Figure 3.5 for a single-electron reaction. Since we are only interested in energy differences, we have arbitrarily set the energy of the reduced state to be the same for the two curves. The upper curve is at a lower (more negative) potential since a decrease in potential corresponds to an increase in the energy of the electrons. Therefore, the energy is higher for V₁ (the lower potential)_, and ΔV = V₂ − V₁ > 0.

The reduction reaction represented by Equation 3.3 takes place as one moves along the reaction coordinate from the left to the right of the diagram. At an electrode potential of V₁, the reduction reaction is favored as the energy of the reduced state is lower than that of the oxidized state. The activation barrier for the reduction is also lower than that for oxidation (the reverse reaction). However, the situation changes when the potential of the electrode is changed from V₁ to V₂ so that the oxidation reaction becomes favored by the increase in potential (see Figure 3.5).

The potential change from V₁ to V₂ affects the energy of an electron in the oxidized state relative to that in the reduced state by FΔV. The activation energies of both the reduction (cathodic) and oxidation (anodic) reactions are also changed. We define β as the fraction of the total energy change that impacts the activation energy for the cathodic reaction and (1 − β) as the fraction that impacts the anodic activation energy. Therefore, the shift in potential from V₁ to V₂ changes the activation energies as follows for the single-electron reaction under consideration:

For the cathodic reaction:

(3.5)

and for the anodic reaction:

(3.6)

where c represents cathodic, a represents anodic, and ΔV is positive since V₂ > V₁. We can now use Equation 3.5 to write an expression for the cathodic reaction at potential V₂:

(3.7)

Since the precise values of V₂ and V₁ are arbitrary, we can define a reference potential so that V₁ is equal to zero. The activation energy at the reference potential () can then be treated as a constant and be incorporated into the rate constant . We can also drop the subscript on V₂. This convention leaves us with the following expression for the cathodic reaction:

(3.8)

We can now use this equation to write an expression for the cathodic current density. Note that the direction of cathodic current is from the solution to the electrode (electrons move in the direction opposite to the current or, in this case, from the electrode to the species in solution that is reduced). Cathodic current is negative by convention. Consistent with this convention and the transfer of a single electron,

(3.9)

Following a similar procedure, we obtain the following for the anode:

(3.10)

At the equilibrium potential, U, the net current is zero and the magnitude of the anodic current is equal to that of the cathodic current. This value of the current density at equilibrium is defined as the exchange-current density, i_o (remember that the net current is zero). Therefore,

(3.11)

If we multiply and divide Equation 3.10 by the anodic expression for i_o, we obtain

(3.12)

which simplifies to

(3.13)

The above procedure yields a similar expression for the cathodic current density:

(3.14)

We now define the surface overpotential, η_s, which is the driving force for the reaction:

(3.15a)

where V and U are the potential and equilibrium potential relative to the same reference electrode located just outside the double layer. As such, these potentials are measurable and well defined. η_s is also equal to the difference between the voltage drop across the double layer at the potential of interest (not measurable) and the voltage drop across the double layer at equilibrium (also not measurable). The choice of reference electrode is arbitrary since both V and U are referred to the same reference. The surface overpotential is quite important and will be used repeatedly throughout the course.

Although the definition of the surface overpotential in Equation 3.15a is adequate for many problems, it is often necessary to fix further the value of the potential when analyzing more complex systems. To facilitate this, it is useful to further expand our expression for η_s as follows:

(3.15b)

where ϕ₁ is the potential of the electrode (e.g., metal) and ϕ₂ is the potential measured by a specific reference electrode located in the solution just outside the double layer. U is the equilibrium potential defined against that same reference electrode. Be careful since the value of U will change with the reference electrode chosen.

We can now write the expression for the net current density by combining Equations 3.13, 3.14 and 3.15a:

(3.16)

This equation is known as the Butler–Volmer (BV) equation, shown here for an elementary reaction involving the transfer of a single electron. The value of β for this type of reaction is typically ∼0.5. A derivation similar to that provided above can be performed for any elementary reaction, and procedures have been developed to handle sets of elementary reactions.

The form of Equation 3.16 is useful for describing a wide variety of elementary and nonelementary reactions and is used broadly in electrochemical engineering. It can be generalized by defining anodic and cathodic transfer coefficients α_a and α_c to yield

(3.17)

which is a frequently used form of the BV equation. Note that α_a + α_c = n is generally true, where n is the number of electrons transferred in the reaction of interest.