In this section, we examine Faraday’s law, which is the relationship between the amount of current that flows through the external circuit and the amount of material that is either consumed or produced in a half-cell reaction. To explore how this works, let’s return once again to the zinc reaction:
(1.6)![]()
From the half-cell equation, it is apparent that two electrons are produced for every zinc atom that reacts. Typically, it is more convenient to work in terms of moles rather than atoms. Therefore, two moles of electrons are produced for every mole of zinc atoms that is oxidized. As you can see, we can easily relate the moles of electrons to the moles reacted or produced for any species in a given half-cell reaction.
The next step is to relate the moles of electrons to the current that we measure through the external circuit. To do this, it is customary to introduce a new unit of charge—an equivalent. An equivalent is defined as a mole of charge (either positive charge or negative charge, it does not matter). The number of equivalents of a compound is simply the amount of the substance (in moles) multiplied by the absolute value of its charge, zi. For instance, one mole of Na+ is 1 equivalent, whereas one mole of Ca2+ would be 2 equivalents. Because the sign of the charge does not matter, one mole of electrons is equal to 1 equivalent of charge.
The external current is expressed in amperes [A or C·s−1]. Therefore, we need a relationship between coulombs [C] and equivalents. That relationship is called Faraday’s constant, F, which has a value of 96,485 C/equivalent. Faraday’s constant can also be expressed in terms of two other constants: the fundamental unit of charge, q, and Avogadro’s number, NAV,
(1.7)![]()
This expression is another way of stating that an equivalent is a mole of charge, since q is the amount of charge on a proton in coulombs. We also need a relationship between the current, I [A], and the total charge passed in coulombs. That relationship is
where Q is the charge in [C], I in [A], and t in [s]. In situations where the current is constant, Equation 1.8 simplifies to
We now have the pieces that we need to write the relationship between the current in the external circuit and the amount of a substance that is either reacted or produced. Let’s apply what we have learned to the zinc electrode.
ILLUSTRATION 1.2
For the oxidation of zinc, a current of 12 A passes for 2 hours. How much zinc reacts? Provide the answer in terms of mass and the moles of zinc. The reaction is
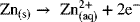
First, the total charge passed is determined from Equation 1.9.
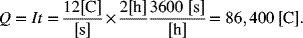
The number of moles of zinc is proportional to the charge passed. From the stoichiometry of the oxidation reaction, for each mole of zinc two moles of electrons are released. Thus,
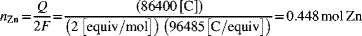
The mass of zinc consumed is simply the moles times the molecular weight:
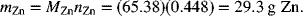
Let’s now generalize what we have done to this point. Any half-cell reaction can be expressed in the following form:
where ![]() is the stoichiometric coefficient for species i, which can be either positive or negative, Ai is the symbol for the specific species (e.g.,
is the stoichiometric coefficient for species i, which can be either positive or negative, Ai is the symbol for the specific species (e.g., ![]() ), and n is the number of electrons involved in the reaction. The mass of species i that is either consumed or produced is equal to
), and n is the number of electrons involved in the reaction. The mass of species i that is either consumed or produced is equal to
where ![]() is the molecular weight of species i. This equation is known as Faraday’s law. We have been careful to include the stoichiometric coefficient with Equation 1.11a. However, most often Faraday’s law is written as
is the molecular weight of species i. This equation is known as Faraday’s law. We have been careful to include the stoichiometric coefficient with Equation 1.11a. However, most often Faraday’s law is written as
We will also use this form. When using Equation 1.11b, you need to recognize that n represents the number of electrons per species i. Look carefully at the examples that follow.
Although Equation 1.11 is useful, the most important aspect of this section is the process that we used to develop the equation. We started with charge, Q, in standard units of [C]. This charge is directly related to the current that we measure in [A] as a function of time. We then converted that charge to moles of electrons (equivalents). The moles of electrons were then related through the half-cell reaction to the moles of species i that were either reacted or produced. Finally, we used the molecular weight to convert moles to the desired mass of species i.
A similar procedure can be used to calculate quantities such as the total moles reacted, the molar rate of reaction, or the molar flux due to reaction at the surface. The use of Faraday’s law and the more general procedure used to derive it are demonstrated in Illustration 1.3.
ILLUSTRATION 1.3
For a lead–acid battery, calculate the rate at which Pb reacts and H+ is consumed for a cell operating at 20 [A]. Express the rate of reaction in terms of a molar reaction rate.
The overall reaction for discharge is
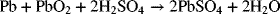
The reaction at the positive electrode is
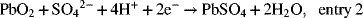
at the negative electrode
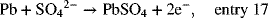
The molar reaction rate of Pb (lead) consumption is obtained from Equation 1.11, Q is replaced with I to convert to a rate, and the molecular weight is not needed:
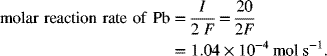
The molar reaction rate of H+ is also obtained from Equation 1.11 in a similar fashion. However, the n value is different. In this case, we have 2 equivalents of charge (the 2 electrons in the half-cell reaction) for every 4 moles of H+. Therefore, n for H+ is 2/4 or 1/2 [equiv mol−1 H+].
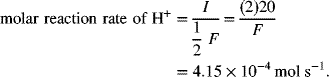
Note that sulfate ions are produced at both electrodes. Based on the stoichiometry for the overall reaction, we expect 2 moles of sulfate ion to be consumed for each mole of Pb. Or, we can say that one mole of electrons react for each mole of sulfate. Formally, this is written as
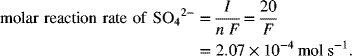
Finally, we note that the reactants and products may be charged or neutral. They can also take several forms, such as a species dissolved in the electrolyte, a solid that deposits on the electrode, or a gas. Illustration 1.3 involved a solid reaction product, PbSO4(s). Now let’s consider the oxidation of chloride ions in solution to form chlorine gas:
Two chloride ions from solution each give up one electron and they combine at the metal surface to form the gas.
ILLUSTRATION 1.4
A current of 20 [A] passes for 10 minutes. How many grams of chlorine gas are produced assuming Equation 1.12 represents the electrode reaction? For ideal gas behavior, what volume of gas does this represent at atmospheric pressure (100 kPa) and at 25 °C?
Use Equation 1.11, n = 2, ![]() = 1,
= 1, ![]() = 70.906 g·mol−1:
= 70.906 g·mol−1:
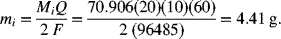
The mass of Cl2 is converted to moles (4.41/70.906), and the ideal gas law (![]() ) is used to determine the volume:
) is used to determine the volume:
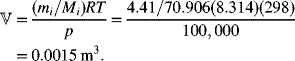

Leave a Reply