Expression for Cell Potential

Note that Equation 2.3 relates the Gibbs energy to the cell potential, U, which is the difference between the potential of the two electrodes. From a practical standpoint, that potential will be positive if you measure it one way, and negative if you switch the wires and measure it again. The fact that the potential can be measured either way illustrates the need to establish a convention so that the connection between the half-cell reactions, the cell potential, and the direction of the full-cell reaction is clear. To do this, we use a diagram similar to that illustrated in Figure 2.1 for a Daniell cell consisting of a zinc electrode in a zinc sulfate solution on one side of a semipermeable separator, and a Cu electrode in a copper sulfate solution on the other. The physical device (left side) is represented as the cell (right side) for thermodynamic analysis.

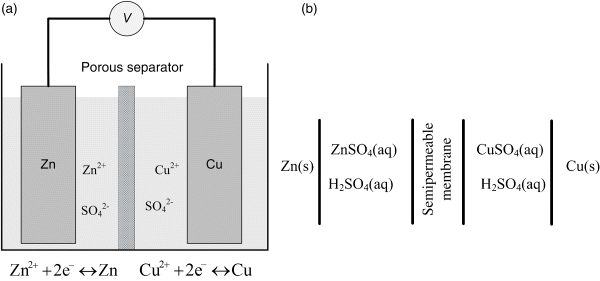
The vertical lines in the cell diagram indicate phase boundaries. In this example, we have four phase boundaries and five phases. On the left is zinc metal. The zinc electrode is in contact with an aqueous solution of zinc sulfate, which does not conduct electrons but allows for ions to move between the two metal electrodes. For simplicity, here we assume that the zinc sulfate solution is separated from the copper sulfate solution by a semipermeable membrane. This membrane allows for the transport of sulfate ions, but excludes all other species. Recall that at least one species is absent from each electrode. At the interface between the Zn and the solution of zinc sulfate, copper ions are absent. On the other side, zinc ions are absent. On the right is the copper electrode, which is more positive at standard conditions as we’ll see shortly. The two electrochemical half-cell reactions are

(2.4)

and

(2.5)

The bidirectional arrow is used to emphasize the fact that each half-cell reaction is at equilibrium. By convention, the equilibrium potential of the cell, U, is equal to the potential of the electrode on the right minus the potential of the electrode on the left, or

(2.6)

Since we generally define U so that it is positive, we put the more positive electrode on the right and the negative electrode on the left as shown in Figure 2.1. At this point, it is instructive to consider briefly what happens when the circuit is closed and a small amount of current is allowed to flow. Electrons naturally flow from low to high potential because of their negative charge. Therefore, if U is positive, the electrons would flow from the electrode on the left to the electrode on the right when the circuit is closed. Applying this knowledge to the cell considered above, we see that oxidation is occurring at the left electrode; that is, the left electrode is giving up electrons. Conversely, reduction is occurring at the right electrode:

(2.7)

and

(2.8)

Thus, the spontaneous path is for zinc to be oxidized at the electrode on the left, and copper to be reduced at the other electrode.

(2.9)

In other words, the direction of the spontaneous full-cell reaction that correctly corresponds to the cell potential is obtained by writing the reaction on the right as the cathodic reaction and that on the left as the anodic reaction. We now have a well-defined connection between the half-cell reactions, the overall or full reaction for the cell, and the equilibrium cell potential. In addition, Equation 2.3 provides a relationship between the Gibbs energy of the reaction and the equilibrium potential of the cell.

How can we use this information to determine the equilibrium potential of the cell? To answer this question, we next write the following expression for ΔG:

(2.10)

where  is the Gibbs energy change for the reaction at standard conditions, a_i is the activity of species i, and s_i is the stoichiometric coefficient of species i in the reaction (positive for products and negative for reactants) at the conditions of the cell. Because it is infeasible to measure and list the Gibbs energy for every reaction under every set of conditions, we tabulate the Gibbs energy at an arbitrary standard condition (25 °C, 1 bar) for species in a reference state (more on this later), and then correct this value for the particular conditions of interest. Combining Equation 2.10 with Equation 2.3 yields

(2.11)

where  is the standard potential for the full cell () at 25 °C and is defined at the same standard conditions as . Also, similar to ,  is not an absolute quantity, but a difference or relative value. One way to determine the standard potential for the full cell is to calculate it from the standard change in Gibbs energy for the reaction. However, it is often easier to use tabulated values of the standard potential for the reactions of interest as described in the next section.