In dilute solutions, long-range electrical interactions between ions dominate, and the activity coefficient can be estimated from a determination of the electrical contribution alone. The chemical potential is equal to the reversible work of transferring 1 mol of the species to a large volume of the solution at constant temperature and pressure. The nonideal portion for dilute electrolytes is the electrical portion, which is the work required to charge 1 mol of ions in a solution where all of the other ions are already charged. This work can be calculated directly from the Debye–Hückel potential distribution that we determined earlier in Section 2.13. The result is

(2.59)

where the variables were defined in Section 2.13. Since , it follows directly that

(2.60)

The expression on the right arises after introducing the following definitions:

(2.61)

(2.62)

(2.63)

Finally, we can express the mean activity coefficient as

(2.64)

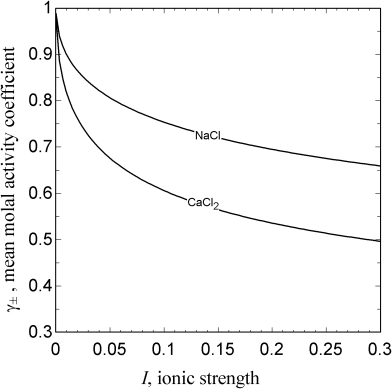
where a is the mean ionic radius of the two hydrated ions. This equation utilizes the relationship shown in Equation 2.55 and takes advantage of the fact that . Ionic strength is the key solution property, which depends on the amount of solute. The only other two parameters are the solvent density and the permittivity. Figure 2.8 shows the activity coefficient as a function of ionic strength for two salts in water. Thus, we can see that the activity coefficient is always less than one, and for dilute solutions, the logarithm of the activity coefficient is proportional to the square root of ionic strength. Also note that at the same ionic strength the 1 : 2 electrolyte has a lower activity coefficient (i.e., is more nonideal). As the ionic strength approaches zero, the limiting form of Equation 2.60, known as Debye–Hückel limiting law, is

(2.65)

In spite of the approximations made in the derivation, the Debye–Hückel model represents the activity coefficients reasonably well for dilute solutions. In fact, the limiting law is usually within 10% of measured values for concentrations less than 0.1 M. Equation 2.64 further increases accuracy. The size parameter is usually treated as a fitting parameter, although it approximates the expected sizes of ions with typical values from 0.3 to 0.5 nm.

Beyond Debye–Hückel Theory

Debye–Hückel theory considers only long-range interactions between ions, and does not treat ion–solvent interactions or short-range interactions between ions. Therefore, it does not perform well for solutions at concentrations where these additional effects are important. Its shortcomings are evident from the measured behavior for electrolytes at finite concentrations. For example, some electrolytes show large positive deviations from ideality (γ_± ≫ 1), which cannot be described by the Debye–Hückel model.

Many different approaches have been used to describe the activity of electrolytes at higher concentrations. The resulting models correctly represent the asymptotic behavior shown in the Debye–Hückel model while adding framework to account for other important interactions. A full treatment of these models is beyond the scope of this text; however, a generalization or two is appropriate. First, predictive capability is limited, and all of the models depend to one degree or another on empirical data for parameter fitting. Second, most of the models are interpolative in nature and are generally applicable to binary electrolytes. They provide precise interpolation over the range of conditions for which they were fit, often with a minimum number of parameters; however, they are not intended for extrapolation outside of this range. Note, also, that the ability of different models to effectively model temperature-dependent behavior varies. The bottom line is that data have been measured for many binary electrolytes, and a number of different types of models have been used to successfully fit those data over a broad range of concentrations.

The situation is different for multicomponent solutions where the mean ionic activity coefficient, , is not appropriate, and the activity of a given ion is influenced by all of the different types of ions in solution. In this situation, it is necessary to approximate single-ion activity coefficients for the multicomponent system of interest. To do this, Newman describes a method to approximate the activity coefficient of ions in a moderately dilute multicomponent solution using parameters from the corresponding binary systems. Under certain conditions, Meissner’s corresponding states model can be extended to predict multicomponent systems from binary system parameters for a broad range of concentrations. Local composition models for electrolytes are extensions of similar types of models for nonelectrolytes and have built-in generalization to multicomponent solutions. The most used of these models is perhaps the model of Chen and Evans, which is included as part of a popular process simulation program where it is used to handle electrolyte thermodynamics. This model has been used successfully for many different systems over a broad range of concentrations.

ILLUSTRATION 2.8

Calculate the activity coefficient for aqueous 0.1 molal solutions of NaCl and CaCl₂ using the Debye–Hückel approximation. Use a permittivity of 6.9331×10⁻¹⁰ F m⁻¹. The two solvent constants for water at room temperature are

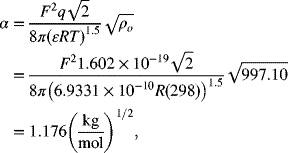
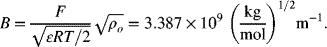
The ionic strength is given by Equation 2.61. For a 0.1 molal solution,  

The values for Ba are reported as 0.9992 and 1.536 for NaCl and CaCl₂, respectively. From Equation 2.64 the mean activity coefficients are  and .

Closure

The focus of this chapter has been on the potential of electrochemical cells at equilibrium. Specifically, we have shown how to relate this potential to the environmental conditions at the electrode: temperature, pressure, and composition. Principles of classical thermodynamics have provided the framework for these calculations. The reference electrode has also been introduced. The potential measured with a reference electrode will be a critical variable for subsequent chapters.

Further Reading

1. Bard, A.J., Parsons, R., and Jordan, J. (Eds.) (1985) Standard Potentials in Aqueous Solutions, Marcel Dekker, New York.
2. Ives, D.J. and Janz, G.J. (Eds.) (1961) Reference Electrodes Theory and Practice, Academic Press, New York.
3. S. A. Newman (Ed.) (1980) Thermodynamics of Aqueous Systems with Industrial Applications, ACS Symposium Series, 133, American Chemical Society.
4. Newman, J. and Thomas-Alyea, K.E. (2004) Electrochemical Systems, John Wiley & Sons, Inc., Hoboken, N. J.
5. Pourbaix, M. (1974) Atlas of Electrochemical Equilibria in Aqueous Solutions, NACE, Houston.
6. Tester, J.W. and Modell, M. (1996) Models of electrolyte solutions, in Thermodynamics and Its Applications, Prentice Hall.

Problems

2.1. Write the associated electrochemical reactions and calculate the standard potential, U^θ from ΔG° for the following cells:

1. Chlor-alkali process to produce hydrogen and chlorine from a brine of NaCl (aqueous salt solution). Use the hydrogen reaction for an alkaline solution.
2. Acetic acid/oxygen fuel cell with acidic electrolyte, where the acetic acid reacts to form liquid water and carbon dioxide. The reaction at the negative electrode is

2.2. Does the redox reaction as written below proceed spontaneously at 25 °C and standard conditions?

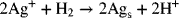
2.3. What is the standard half-cell potential for the oxidation of methane under acidic conditions? The reaction for methane is as follows:

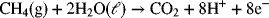
Which element is oxidized and how does its oxidation state change?

2.4. What is the standard cell potential for a methane/oxygen fuel cell? The oxidation of methane produces CO₂ as shown in Problem 2.3, but here assume the product water is a gas, rather than a liquid.

2.5. Let’s consider the oxidation of methane in a fuel cell that utilizes an oxygen conductor (O²⁻) rather than a proton conductor as the electrolyte.

1. At which electrode (oxygen or methane) is O²⁻ produced and at which is it consumed?
2. In which direction does O²⁻ move through the electrolyte? Why?
3. Propose two electrochemical half-cell reactions.
4. Does  change for this fuel cell relative to a fuel cell that utilizes a proton conductor? Why or why not?

2.6. Determine the equilibrium potential of the cell shown below.

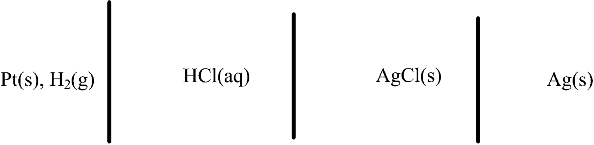
2.7. Consider the electrochemical reactions shown below. Mercury(I) chloride, also known as calomel, is a solid used in reference electrodes. The two reactions are

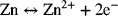
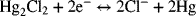
1. What is the overall chemical reaction?
2. Develop an expression for U, the equilibrium potential of the cell.
3. Write down an expression for the standard potential of the cell in terms of the standard Gibbs energies of formation.
4. Use standard half-cell potentials from the table to determine the standard Gibbs energy of formation for aqueous ZnCl₂. Why is this value different than the value for solid ZnCl₂?
5. What is the standard Gibbs energy of formation for Hg₂Cl₂?

2.8. The lithium air cell offers the possibility of a very high-energy battery. At the negative electrode,

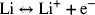
At the positive electrodes, the following reactions are postulated:

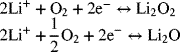
Estimate the standard potential for each of the two possible reactions at the positive electrode paired with a lithium anode.

2.9. Develop an expression for the equilibrium potential for the cell below. The first reaction is the negative electrode of the Edison cell (battery).

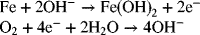
The Gibbs energy of formation for Fe(OH)₂ is −486.6 kJ·mol⁻¹.

2.10. Develop an expression for the equilibrium potential of a hydrogen–oxygen fuel cell operating under acidic conditions. The two electrochemical reactions are

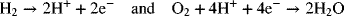
Use the data in the Appendix C for standard Gibbs energy of formation. Compare with the value calculated from standard electrode potentials to identify whether the standard state for water in the table of Appendix A is liquid or gas.

2.11. Write the associated electrochemical reactions, and calculate the standard potential, U^θ, from ΔG° for the following cells:

1. Propane fuel cell with solid oxygen conductor electrolyte.
2. Electrolysis of aluminum, where aluminum is produced from Al₂O₃ and carbon. Note that carbon is oxidized at the anode.

2.12. Calculate the equilibrium potential for peroxide formation in an acid fuel cell

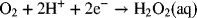
2.13. Use the half-cell reactions for the reduction of cupric ion (Cu²⁺) to copper metal and cuprous ion (Cu⁺) to copper metal to calculate the standard potential for the reduction of cupric ion to cuprous ion. Check your answer against the value given in Appendix A.

2.14. Consider the electrochemical cell below.

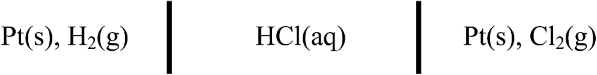
The two reactions are

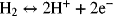
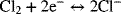
Find an expression for U. If the pressure of hydrogen is 250 kPa and that of chlorine is 150 kPa, what is the numerical value of U at 25 °C in 1 molal HCl? Include the simplified activity corrections (you may neglect activity coefficients).

2.15. Create a Pourbaix diagram for Pb. Treat the following reactions:

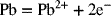
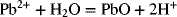
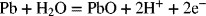
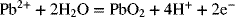
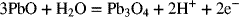
2.16. Create a Pourbaix diagram for Pt. Focus on the low pH range (−2 ≤ pH ≤ 1), and consider the following reactions:

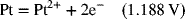
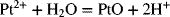
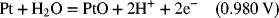
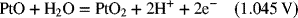
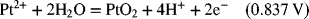
2.17. Create a Pourbaix diagram for Fe. Treat the following reactions:

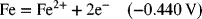
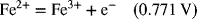
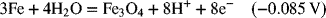
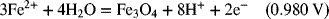
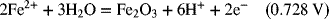
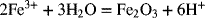
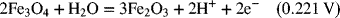
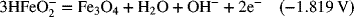
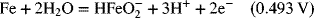
2.18. Use the information in Appendix A to determine the dissociation constant for water, K_w.

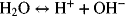
2.19. Determine the solubility product K_sp for PbSO₄.

2.20. Estimate the equilibrium constant for the disproportionation of copper.

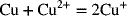
2.21. Explain what a liquid junction is and why the potential of cells with liquid junctions cannot be determined from thermodynamics alone.

2.22. LiPF₆ is a common salt used in lithium batteries. For lithium hexafluorophosphate, LiPF₆, dissolved in propylene carbonate, calculate the Debye length and the activity coefficient (using Debye–Hückel theory) of LiPF₆ at 30 °C. The concentration is 0.1 M. The dielectric constant, ɛ_r  ɛ/ɛ_o, for the solvent is 64 and the density 1.205 g·cm⁻³. The density of the 0.1 M electrolyte is 1.286  g·cm⁻³.

2.23. Consider the electrochemical cell below. Iron corrodes to form Fe²⁺. Develop an expression for U, and determine the value of the standard potential.

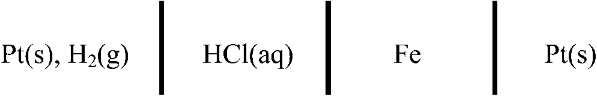
2.24. Find the expression for the equilibrium potential of the cell at 25 °C.

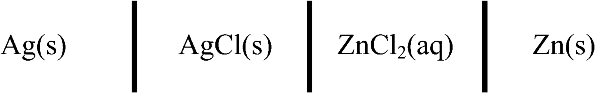
The two electrochemical reactions are as follows:

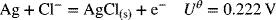
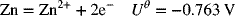
2.25. Calculate the activity coefficient for (a) 0.05 m Cs₂SO₄ and (b) 0.05 m BaCl₂ in water at 25 °C.

Use the following for Debye–Hückel constants (note that Ba is the product of B and a).

For Cs2SO4	Ba = 1.328 (kg·mol−1)1/2
For BaCl2	Ba = 1.559 (kg·mol−1)1/2

2.26. Use the Debye–Hückel theory to calculate the activity coefficient for 0.1 m MgCl₂. in water at 25 °C. Use the following ionic radii for the two ions: Mg²⁺ = 8 Å, Cl⁻ = 3 Å.

2.27. The following activity coefficient data have been measured for NaCl solutions as a function of molality (radius for Na⁺ = 4 Å, Cl⁻ = 3 Å). The temperature is 25 °C. Please do the following:

1. Use the Debye–Hückel theory to calculate the activity coefficients.
2. Use the Debye–Hückel limiting law to calculate the activity coefficients.
3. Compare the results of (a) and (b) with the experimental data and comment on the applicability of the Debye–Hückel equations.mγ_±0.0010.9650.0050.9270.010.9020.050.8210.10.77810.657

2.28. Before concerns about mercury became widespread, the calomel electrode was commonly used. Crystals of KCl are added to produce a saturated solution. What advantage does a saturated solution provide? The saturated calomel electrode has an equilibrium potential of 0.242 V, which is lower than the standard potential of 0.2676. Can this 25 mV difference be determined from thermodynamics? Why or why not? The solubility of KCl in water at 25 °C is 360 g KCl per 100 g water.

2.29. A solid oxide fuel cell operates at 1000 °C. The overall reaction is

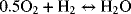
1. Calculate the standard potential at 25 °C assuming that reactants and products are gases.
2. Calculate the standard potential at 1000 °C using Equation 2.18.
3. Using the correlation for heat capacity as a function of temperature shown below, calculate the standard potential at 1000 °C. Comment on the assumption used in part (b) that ΔS° is constant.A [J·mol⁻¹·K⁻¹]10³B [J·mol⁻¹·K⁻²]10⁻⁵C [J·K·mol⁻¹]H₂O30.5410.290O₂29.964.184−16.7H₂27.283.260.50

2.30. Alloys of LiSn are possible electrodes for batteries. There are many phases possible, but we want to focus on the reaction

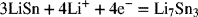
The standard potential of this reaction at 25 °C is 0.530 V (versus reference Li electrode). If the enthalpy of the reaction

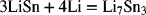
is −226 kJ·mol⁻¹ Li₇Sn₃, estimate the standard potential at 400 °C.

2.31. Find the equilibrium constant, K_eq, for Pt dissolution reaction at 25 °C.

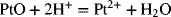
The following thermodynamic data are provided, ⁻¹, and

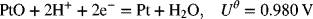
2.32.

1. Write the overall reaction and determine the standard potential for the lead–acid battery.
2. Develop an expression for the equilibrium potential, U, for the lead–acid battery as a function of electrolyte composition. The final expression should include the molality and activity coefficient.
3. The potentials of the two electrodes relative to a Hg-Hg₂SO₄ reference electrode at 25 °C has been measured. What is the likely reaction at the reference electrode? If the standard Gibbs energy of formation of Hg₂SO₄ is −625.8 kJ·mol⁻¹ and the standard Gibbs energy of formation of  is −744.62 kJ·mol⁻¹, determine the standard potential of the positive (lead oxide electrode) relative to the reference electrode. How does this value compare to the measured value of 0.96 V? Explain the possible cause of any difference.
4. Given that the potential difference between the positive electrode and the reference electrode is 1.14 V, estimate the activity coefficient for sulfuric acid () at 6 m. For this evaluation, you may assume that the activity of water is one.
5. Does the potential of the lead electrode (Pb) relative to the reference electrode depend on the molality of the sulfuric acid? Explain your answer.

2.33. Rework Illustration 2.7 (reference electrode example) with a Ag₂SO₄ reference electrode rather than a Hg₂SO₄ reference electrode. The standard potential for this reference electrode reaction (below) is 0.654 V.