In this chapter, we have shown how to calculate the thermodynamic potential and the relationship between this equilibrium value and the change in the Gibbs energy for the full-cell reaction. We have also referred to this potential as an equilibrium potential. Clearly, however, the full-cell reaction is not in equilibrium, which would mean that ΔGRx = 0. Why, then, do we refer to this potential as the equilibrium voltage? What exactly is in equilibrium?
When there is no flow through an external circuit, then the half-cell reaction at each electrode approaches equilibrium. At equilibrium, the energy of the electrons in the metal is characteristic of the reaction, and related to the standard potential—more on this in a minute. First, what does it mean to approach equilibrium, and what exactly is in equilibrium?
An example in the form of a thought experiment may be helpful at this point. Let’s imagine that we have a copper metal electrode in an acidic sulfate electrolyte. If the Gibbs energy for dissolution of the metal is negative, then some of the copper atoms will give up their electrons, leave the copper metal lattice, and move into solution as cations. This leaves excess charge in the copper metal, resulting in an increase in the electron energy. The addition of cations to the solution increases the copper ion activity. Since the half-cell reaction of interest is
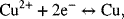
both the increase in electron energy and the increase in copper ion activity increase the rate of the reduction reaction relative to that of the oxidation reaction. The process continues until equilibrium is reached and the rates of the forward and reverse reactions are equal. While the above is a simplification of the actual physics, it provides a conceptual context for understanding the equilibrium of half-cell reactions. Thus, the half-cell voltage really does represent the equilibrium point for the reaction of interest on the hydrogen scale.
The Gibbs energy change, 
is equal to zero for a half-cell reaction at equilibrium, which is approached under open-circuit conditions. At constant T and p, the Gibbs energy change for the reaction can be expressed in terms of the electrochemical potentials of the species that participate in the reaction:
where 
is the stoichiometric coefficient for species i as we have defined and used it previously in this book. The electrochemical potential, 
, is defined as
which includes a chemical portion (
) and an electrical portion (
). The chemical portion is the chemical potential about which you may have learned in a course on chemical thermodynamics. The electrical portion represents the work required to bring a charge from infinity to a location inside the solution, and is known as the Galvani potential or inner potential. It is equal to zero for uncharged species. It is also zero for charged species in a bulk solution with no electric field or without surfaces where charges align to create fields. Thus, the columbic interactions of ions in a neutral bulk solution are included in the chemical term. In contrast, the impact of the electric field on ions in solution due to, for example, charge on the electrodes, is included in the electrical portion of the electrochemical potential.
Application of Equations 2.29 and 2.30 to the copper reaction yields, at equilibrium:
where
(2.31c)
since the copper metal and the electrons are assumed to be in their standard state. Substituting Equations 2.31b–2.31d into Equation 2.31a and rearranging yields
(2.33)
where 
is the potential difference between the metal and the solution under standard conditions. The quantity 
is the potential difference across the interface at equilibrium. This interfacial potential plays an important role in electrochemical systems. For example, a potential difference across the interface that is greater than the value at equilibrium will cause the reaction to take place in the anodic direction. Conversely, the cathodic reaction will take place if the potential across the interface is less than the equilibrium value. We will examine this again in Chapter 3 when we discuss reaction kinetics. The purpose of this section was to illustrate the role of the potential in establishing interfacial equilibrium for single electrochemical reactions. This, of course, is unique to electrochemical reactions.
Unfortunately, 
is not accessible experimentally, since there is no way to measure the solution potential without introducing another interface, and therefore another interfacial potential drop, into the system. Consequently, how do we measure and quantitatively characterize the equilibrium potential for a half-cell reaction? We have already seen the results of the answer to this question. Since we can measure the potential between two electrodes, and we know that reversible half-cell reactions are at equilibrium at open circuit, we simply define a half-cell as our reference point and measure all other potentials relative to that reference. As long as the reference half-cell reaction remains at equilibrium, the process of defining a reference electrode is equivalent to adding a constant to the potential across the interface of the electrode of interest. The universal reference is the SHE, whose potential has been defined as zero. The hydrogen reaction is often highly reversible and reproducible. The potential of an electrode relative to a hydrogen electrode is measurable. Also, by making appropriate corrections, the potential of an electrode measured in a practical system relative to any other electrode at equilibrium can be quantitatively related to the potential of that electrode versus SHE. Thus, we have a well-defined way of determining the equilibrium potential of a half-cell reaction.
Leave a Reply