We end this chapter with an example of an industrial electrolytic process—chlorine production by the chlor-alkali route. Our objectives in this section are twofold. First, to review principles and terminology within the context of an important electrochemical system. Second, to introduce the concept of the current–voltage relationship, also called the I–V curve. The connection between current and voltage is essential to any analysis of electrochemical systems. Finding and understanding this I–V relationship is a persistent theme of the book.
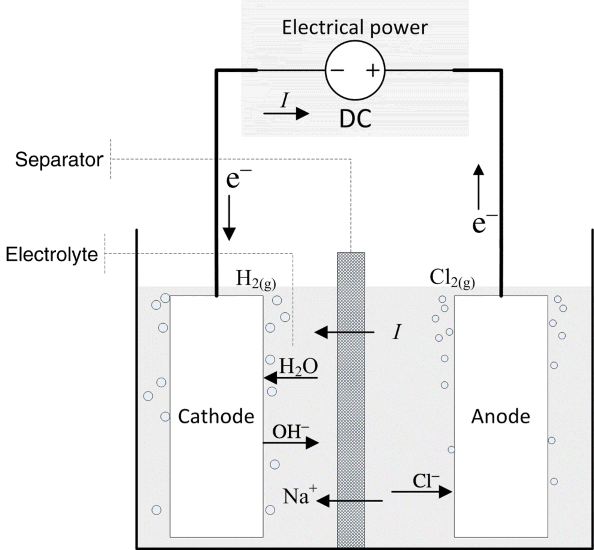
A simple representation of the electrochemical system for the chlor-alkali process is shown in Figure 1.4. The overall reaction can be written as
In order to operate without interruption, reactants are supplied and products removed continuously. The reactant stream for the process is a purified brine of sodium chloride (NaCl), essentially a concentrated solution of salt water. The solution flows at a steady rate into the electrochemical cell, also called the electrochemical reactor. In addition to chlorine gas, sodium hydroxide and hydrogen are produced simultaneously in the process. Despite the appearance from the above equation, this reaction does not occur homogeneously. Instead, two heterogeneous electron-transfer reactions take place on separate metal surfaces:
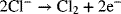
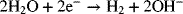
The two metals on which the reactions occur are the electrodes, which are inert since they do not participate in the reactions. The electron-transfer reactions are faradaic processes and are governed by Faraday’s law. Oxidation takes place at the first electrode of our example, where two chloride ions lose electrons to form chlorine gas. Therefore, this electrode is the anode. The electrons enter the metal and travel through an external circuit. At the other electrode, the cathode, water is reduced to form hydrogen gas. The electrons consumed at the cathode are supplied by the external circuit, and the number of electrons produced at the anode is the same as the number consumed at the cathode. The electrolyte that is between the two electrodes contains ions of Na+, Cl−, and OH−. In this instance, there is a membrane separator that serves two functions: It keeps the two gaseous products apart and it allows sodium ions to move from the anode compartment to the cathode compartment, but excludes transport of anions. It is this movement of sodium ions that carries the current in the electrolyte. Note that there are three phases: solid (electrodes), liquid (electrolyte), and gas (reaction products). Furthermore, not all species are present in every phase. For instance, free electrons are found only in the metals, ions are confined to the electrolyte, and hydrogen gas is limited to the cathode. This heterogeneity is one of the defining characteristics of electrochemical systems—Almost all of the action occurs at interfaces between the electrode and the electrolyte.
As you are probably beginning to appreciate, electrochemical systems are inherently complex. We’ve already seen that both electrodes are necessary and must be considered together. Many things happen at once: electron transfer, adsorption and desorption, transport of reactants and products, current flow in the electrolyte, and surface-mediated combination. In order to understand and analyze electrochemical systems, we’ll need to simultaneously apply our knowledge of thermodynamics, kinetics, and transport. These fundamental topics will be considered systematically in the chapters that follow.
Electrochemical cells are sometimes broken into two categories: galvanic and electrolytic. The two types have more similarities than differences, and are governed by the same engineering principles. The main distinction between them is that energy or electrical work is an output of a galvanic cell (e.g., a fuel cell or a battery discharging), whereas electrical energy is an input to electrolytic cells. We see in Figure 1.4 that a direct current (DC) power supply adds electrical work in the chlor-alkali process; therefore, this process is electrolytic.
An important feature of electrochemical systems is that current is an expression of the rate of reaction. In our example, the electrical current through the cell is directly related to the formation and consumption rates of hydrogen, chlorine, and sodium chloride through Faraday’s law. We can control the rate of reaction by controlling current. How much work is associated with this current flow? To answer this question, we need to know the potential of the cell. The potential is an expression of energy for charged species (electrons and ions), and provides the driving force needed for electrochemical reactions and for the flow of current in both metals and electrolytes.
We cannot simultaneously control the potential and current of an electrochemical system. If the potential applied to our electrolysis cell is increased, then the rate of hydrogen/chlorine production will also be increased. Alternatively, we might establish the rate of production by setting the current, but we would need to accept the resulting potential. These are the two basic modes of operation for electrochemical cells: potentiostatic (constant potential) or galvanostatic (constant current).
As mentioned above, a key objective in the analysis of any electrochemical system is to find the relationship between current and potential. The relationship can be complex, but with careful examination of the thermodynamics, kinetics, and mass transport, it can be readily understood. In the first chapters of this book, we will develop the fundamental principles needed. These will systematically be applied to a number of electrochemical systems, and we will return repeatedly to the relationship between the current and voltage as characterized by the I–V curve. Much of this textbook will be dedicated to the development and application of the relationships that describe the current (the reaction rate) as a function of potential (the driving force). You already know one such relationship, the resistor. Using an equivalent form of Ohm’s law (Equation 1.15), we can relate the current and potential for a resistor. If the current density is constant, Equation 1.16 can be written in terms of resistance to give
(1.18)![]()
This equation shows a linear relationship between potential and current density. However, the current–voltage relationship is generally more complex for an electrochemical system, and we will need to use thermodynamics (Chapter 2), electrode kinetics (Chapter 3), and mass transfer (Chapter 4) to describe it. Here, we simply want to introduce some of the basic features of such a curve.
An example of a current–voltage curve is shown in Figure 1.5 for steady-state operation. First, note that when the current density is zero, the potential of the cell is not zero. If the external circuit is open (disconnected), no current flows and we say that the cell is at open circuit. This open-circuit potential is largely determined by thermodynamic considerations and depends on the type of electrode and the composition of the electrolyte near the electrodes. For the chlor-alkali cell, it is about 2 V, as indicated in the figure. This equilibrium potential is the subject of Chapter 2. If the external circuit were simply closed (connected) without a DC power supply, current would flow. However, the reactions would be in the direction opposite to that indicated by Equation 1.17. In other words, chlorine, hydrogen, and hydroxyl ions would spontaneously react to form chloride ions and water, and the potential of the cell would be lower than the equilibrium potential. This situation corresponds to using the chemical energy of the reactants to perform work, and corresponds to a galvanic cell. The difference between the equilibrium or open-circuit potential and the actual cell voltage is called polarization (see Figure 1.5).
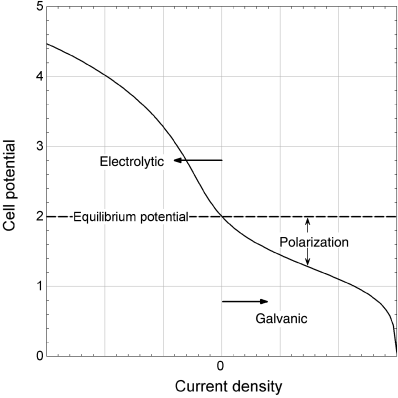
Of course, this is not how a chlor-alkali cell is intended to operate. We want to produce chlorine gas and caustic soda. By the addition of work, we can drive the reaction in the opposite direction, the direction indicated in Equation 1.17. To do this, the cell potential must be greater than the equilibrium potential. Because we are adding work to the cell, we refer to the cell as an electrolytic cell. As shown in Figure 1.4, a voltage source is added to the chlor-alkali cell in order to provide the electrical work needed to drive the reaction in the desired direction. The difference between the cell potential and the equilibrium potential is a measure of how much work or energy must be added to drive the reaction at a particular rate.
Returning to Figure 1.5, which shows the I–V curve for the complete electrochemical cell, we have seen that an electrochemical cell has a nonzero potential at open circuit, where the current is zero. This potential is described by thermodynamics and represents the difference in the energy of electrons in the two electrodes. Operation of the cell in a galvanic mode takes place at cell potentials below the equilibrium potential, and corresponds to the conversion of chemical energy into electrical energy. In contrast, operation of the cell in an electrolytic mode occurs at potentials greater than the equilibrium potential, and requires that energy be added to the cell. In both cases, the difference between the equilibrium potential and the cell potential during current flow is called the polarization. As shown in the figure, the relationship between current and cell potential is, for the most part, nonlinear. The details will be covered in subsequent chapters. Also note that the curve is not symmetric. Although the basic shape of the curve under galvanic operation is similar to that of the electrolytic curve, the details are different.
Closure
In this chapter we have introduced the electrochemical cell and electrochemical systems. Common terminology for electrochemical systems has been presented, and will be used throughout the book. One of the most fundamental concepts, Faraday’s law, was discussed. This law relates electrical charge to the amount of reactants consumed or products produced in an electrochemical reaction, and is essential for the analysis of electrochemical systems.
Further Reading
- LeFrou, C., Fabry, P., and Poignet, C. (2012) Electrochemistry: The Basics with Examples, Springer Berlin.
- Pletcher, D. (2009) A First Course in Electrode Processes, Royal Society of Chemistry, Cambridge.
- West, A.C. (2013) Electrochemistry and Electrochemical Engineering: An Introduction. CreateSpace Independent Publishing Platform.
Problems
1.1. The original “International Ampere” was defined electrochemically as the current required to deposit 1.118 mg of silver per second from a solution of silver nitrate. Using this definition, how does the international ampere compare to the SI version? (Note that the SI version is based on the Ampere force law).
1.2. Molybdenum is deposited from a molten salt. 12.85 g are deposited in 1 hour using a current of 7 A. How many electrons are consumed per mole of Mo reacted? Given that Mo is present in the molten salt as an ion, what is its oxidation state in the molten salt?
1.3. How much hydrogen is needed to operate a 50 kW hydrogen/oxygen fuel cell for 3 hours? The potential of the cell is 0.7 V (remember that Power = IV). The reaction at the anode is
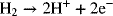
1.4. Calculate the daily aluminum production of a 150,000 [A] aluminum cell that operates at a faradaic efficiency of 89%. The cell reaction is
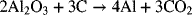
1.5. The annual production of Cl2 is about 45 million tons per year. Assume that a typical plant is operational 90% of the year. The operating voltage of a cell is 3.4 V (considerably higher than the equilibrium voltage).
- Write down the half-cell reaction for the oxidation chloride to form chlorine.
- Determine the total current worldwide needed to generate the global supply of Cl2.
- Calculate the electrical power needed to produce the global supply of chlorine using electrolysis.
1.6. A 25 A current is passed through a molten aluminum chloride melt. What are the likely reactions at the two electrodes? How long must this current be in place to deposit 50 g of Al. During this same time, what is the volume of gas that is evolved at STP (standard temperature and pressure: 273 K, 100 kPa).
1.7. An industrial aluminum cell is operating at 4.2 V with a current of 200 kA. The faradaic efficiency is 95 %, which means that 95% of the current goes to Al production. What is the rate of production of Al in kg per day? The starting material is Al2O3. As an aside, a Boeing 747 aircraft is made from over 60,000 kg of Al.
1.8. Continuous sheet copper is made by electrodeposition from a solution containing CuSO4 onto a rotating drum of lead. For the conditions given below, what should be the rotation speed of the drum (revolution per hour)?
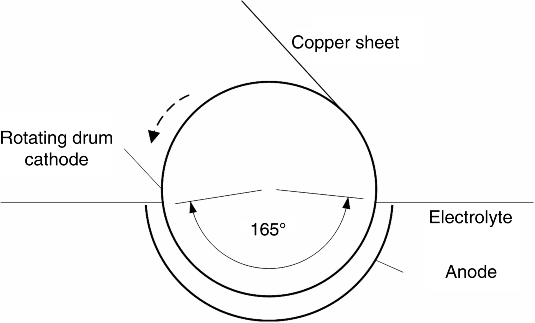
- Cathode current density = 1750 [A·m–2]
- Current efficiency = 95%
- Desired “thickness” (mass per area) = 1.22 [kg·m–2]
- Angle of cathode immersion = 165°
1.9. How many grams of lithium are in a 1320 [mAh] cell phone battery? Note that [mAh] is a unit of charge.
1.10. A plate of steel has lost 50 g to corrosion over the past year. Determine the current that would be associated with this rate of corrosion?
1.11. Corrosion of stainless steel in concrete is an important engineering problem. Because of the long times associated with the low rates of natural corrosion, accelerated testing is often used. One form of accelerated testing is the application of a potential to the metal of interest. However, under the accelerated conditions, the current efficiency may be low. In competition with the oxidation of iron to Fe(II), oxygen can be evolved at high pH:
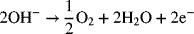
A current of 1.4 mA is passed for 100 hours and the mass loss is 0.11 g. What is the faradaic efficiency for the iron oxidation reaction? How many moles of oxygen are evolved?
1.12. Consider a nickel–zinc battery operating at a current density of 4500 A·m−2. The space between the electrodes is filled with an alkaline electrolyte. If the conductivity of the electrolyte is 60 S·m−1 and the distance between the two electrodes is 2 mm, what is the potential drop across the cell due to ohmic losses?CopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply