Several efficiencies are used to characterize electrochemical processes and systems. The faradaic efficiency was introduced in Chapter 1. Here, we present the current efficiency, which is slightly different:

(3.39)

Undesired reactions occur in both electrolytic and galvanic cells. These unwanted side reactions reduce the current efficiency. We can explore this concept with the charging of a lead–acid battery. Two reactions at the positive electrode are possible. The first is the sought-after reaction for the oxidation of the solid lead sulfate:

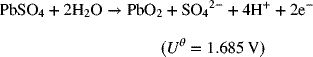
A second, undesired, reaction is the evolution of oxygen:

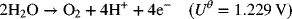
If a certain current is used to charge the cell, what fraction of the electrons produced result from the desired reaction? The answer to this question is determined by the electrode kinetics. Notice that the equilibrium potential for the positive electrode of the lead–acid cell is more than 0.4 V higher that of the oxygen reaction. Thus, we can expect the overpotential for the oxygen reaction to be much larger.

ILLUSTRATION 3.5

Calculate the current efficiency for the positive electrode during charging of the lead–acid cell. At a particular point in the charging process, the overpotential for the oxidation of lead is 0.05 V, and the overpotential of the oxygen evolution reaction is 0.6 V. Use Butler–Volmer kinetics for the reaction with lead.

Kinetic parameters

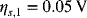
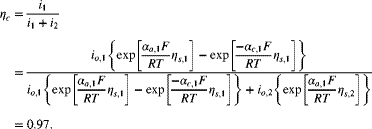
Therefore, 3% of the current is going toward the evolution of oxygen rather than recharging of the battery. Successful operation of this battery relies on sluggish kinetics for oxygen evolution.

Because the current efficiency is not 100%, more current and therefore more energy must be used to charge the battery to the same point. Also, note that current efficiency as defined applies to a single electrode. The current efficiency for the negative electrode of the same battery will be different. Here, the undesired side reaction is the evolution of hydrogen. Because of different transfer coefficients, and different dependencies on temperature, current efficiency can change with polarization.

In subsequent chapters, the current efficiency and some variants will be used for analysis of different electrochemical systems. The focus may be on an electrode, a cell, or even an entire system. As a consequence, it is necessary to modify or even add new definitions. For instance, consider the electrolysis of water to produce hydrogen and oxygen. Even if the current efficiencies of the two electrodes are unity, some oxygen and hydrogen may recombine in the cell and revert to water. This process is clearly undesired and represents a loss that is not captured by the defined current efficiency. The nature of the inefficiency is not electrokinetic, and its discussion is deferred to subsequent chapters.

Closure

The main objective of this chapter was to introduce the relationship between current density and the potential of the electrode. The critical parameter is the surface overpotential, the difference in potential between the metal and the solution just outside of the double layer. In order to remove ambiguity, these potential are measured with a reference electrode. Most of the time, this current−voltage relationship is described with the Butler–Volmer equations. However, it is important to remember that this expression is semiempirical and cannot be expected to apply to every situation. Finally, the potential of full cell that includes kinetic resistance was developed.

Further Reading

1. Bard, A.J. and Faulkner, L.R. (2001) Electrochemical Methods, John Wiley & Sons, Inc., Hoboken, NJ.
2. Delahay, P. (1965) Double Layer and Electrode Kinetics, John Wiley & Sons, Inc., New York.
3. Vetter, K.J. (1967) Electrochemical Kinetics: Theoretical Aspects, Academic Press, New York.

Problems

3.1. The following reaction occurs rapidly at an inert electrode.

The standard potential for the reaction is 0.26 V; 10 mg of potassium ferricyanide is added to 100 cm³ of water.

1. Determine the concentration of K⁺,  at equilibrium if the measured potential relative to a hydrogen reference electrode at 25 °C is 0.26 V.
2. Calculate the Debye length and sketch the potential near the electrode.
3. What is the effect of adding KCl to a concentration of 0.1 M on the Debye length and the electric field across the double layer?

3.2. Repeat Illustration 3.2(a) for the situation where the potential (0.10 V) is relative to a Ag/AgCl reference electrode. The equilibrium potential for the saturated Ag/AgCl electrode is 0.197 V. Please comment on any differences that you observe between the two solutions.

3.3. Hydrogen gassing can be a serious problem for lead–acid batteries. Consider two reactions on the negative electrode: the desired reaction for charging

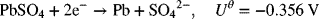
and an undesired side reaction

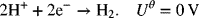
1. The exchange-current densities for the two reactions are , and , where the exchange-current density for the hydrogen reaction is on pure lead. Calculate the current density for each reaction if the electrode is held at a potential of −0.44 V relative to a hydrogen reference electrode. The temperature is 25 °C, and the transfer coefficients are 0.5.
2. With Sb impurity in the lead, the exchange-current density of the hydrogen reaction increases to 3.7 × 10⁻⁴ A·m⁻². Repeat the calculation of part (a) in the presence of antimony. Assuming that all impurities cannot be eliminated, what implications do these results have for the operation of the battery?

3.4. Data for the exchange-current density for oxygen evolution on a lead oxide surface are provided as a function of temperature. Develop an expression for i_o as a function of temperature. What is the activation energy? If the transfer coefficient is a constant at 0.5 and the overpotential is 0.7 V, at what temperature will the current density for oxygen reduction be 5 A·m⁻²?

T [°C]	io [A·m−2]
15	6.9 × 10−7
25	1.7 × 10−6
35	7.6 × 10−6
45	1.35 × 10−5

3.5. The following reaction is an outer sphere reaction that occurs in KOH.

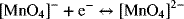
Would you expect the reaction to have a larger or small reorganizational energy compared to an isotope exchange reaction for manganese? What does this imply about the reaction rate?

3.6. On the right find a portion of Julius Tafel’s original data for the evolution of hydrogen on mercury (Zeit. Physik. Chem. 50, 641–712 (1905)). Create a Tafel plot and find the Tafel slope for these data. The experiments were conducted in 2 N sulfuric acid at 26.4 °C.

Potential	Current density [A m−2]
1.665	4
1.713	10
1.7465	20
1.7665	30
1.777	40
1.824	100
1.858	200
1.878	300
1.891	400
1.912	600
1.94	1000
1.963	1400
1.989	2000

It’s interesting that these data were plotted on a linear scale in the manuscript, so Tafel never created the plot named in his honor, but he did report the slope. What additional information would be necessary to determine the exchange- current density?

3.7. The evolution of oxygen is an important process in the lead–acid battery. Assuming that the positive electrode of the flooded lead–acid battery is at its standard potential (entry 2 in Appendix A), calculate the overpotential for the oxygen evolution reaction. It is reported that the Tafel slope for this reaction is 120 mV per decade at 15 °C. What is the transfer coefficient α_a? If the exchange-current density is 6.9 ×10⁻⁷ A·m⁻², what is the current density for oxygen evolution? You may neglect the small change in equilibrium potential with temperature.

3.8. The tabulated data are for the dissolution of zinc in a concentrated alkaline solution. These data are measured using a Hg/HgO reference electrode. Under the conditions of the experiment, the equilibrium potential for the zinc electrode is −1.345 V relative to the HgO electrode.

Potential [V]	i [A·m−2]
−1.335	58
−1.325	150
−1.315	300
−1.305	600
−1.295	1100
−1.285	1970
−1.275	3560
−1.265	6300
−1.255	11,500
−1.245	20,000
−1.235	36,800
−1.225	66,000

1. Please determine the exchange-current density and Tafel slope that best represent these data.
2. For the same electrolyte, the potential of a SCE electrode is 0.2 V more positive than the Hg/HgO reference. If the potential of the zinc is held at −1.43 V relative to the SCE electrode, what is the current density for the oxidation of zinc?

3.9. Derive Equation 3.28. For a reaction at 80 °C, and with (α_a + α_c) = 2, at what value for the overpotential will the error with the Tafel equation be less than 1%?

3.10. In order to model the deposition of copper, the following data have been collected for 1 M CuSO₄ in 1 M H₂SO₄. The temperature is 25 °C, and a copper-plated reference electrode was used. From these data determine the parameters for the Butler–Volmer kinetic expression. The reaction is

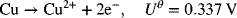
I [A m−2]	ηs [V]	I [A·m−2]	ηs [V]
−300	−0.1004	−40	−0.0192
−250	−0.0919	−2.3	−0.00101
−200	−0.0818	67	0.0192
−150	−0.0717	135	0.0293
−125	−0.0616	250	0.0394
−100	−0.0515	450	0.0495
−75	−0.0414	1100	0.0657

3.11. In Section 3.7, Equation 3.33 was developed using Tafel kinetics, illustrating the effect of mass transfer on the current density. Derive the equivalent expression for linear kinetics. Explain the difference in shape of graphs for i versus η_s between linear and Tafel kinetics.

3.12. Metal is deposited via a two-electron reaction with current voltage data as shown at the right. The equilibrium potential is −0.5 V versus the same reference electrode used to measure the data. The bulk concentration is 100 mol·m⁻³. You may assume that the exchange-current density is linearly dependent on the concentration of the reactant (i.e., you may use Equation 3.33). Assume 25 °C.

Applied potential (versus reference electrode)	Deposition current [A·m−2]
−0.6	−1.2
−0.7	−2.1
−0.8	−13.7
−0.9	−82.2
−1	−245
−1.1	−330
−1.2	−350
−1.3	−360
−1.4	−362

1. Is mass transfer important? If so, please determine a value for the mass transfer coefficient.
2. Assuming Tafel kinetics, find the values of α_c and i_o. Comment on the applicability of this assumption. Can the normal Tafel fitting procedure be used for this part? Why or why not?
3. If the mass transfer coefficient were reduced by a factor of 2 (cut in half), please predict the current that would correspond to an applied potential of −0.9 V.

Additional Hints: You need to consider carefully which points you use in fitting the kinetic parameters. Also, it is a good idea to normalize the error when fitting the current.

3.13. Use the following property data for a hydrogen−oxygen fuel cell at 25 °C.

Oxygen electrode	Hydrogen electrode	Electrolyte
io = 9 × 10−7 A·m−2	io = 14,000 A·m−2	κ = 10 S·m−1
αa = 3, αc = 1	αa = , αc = 1	L = 40 μm
U = 1.229 V	U = 0 V

1. Operating at a current density of 10,000 A·m⁻², calculate the potential of the full cell, V_cell.
2. Can the kinetics be simplified for either electrode, or is the complete Butler–Volmer kinetics needed?

3.14. For the Ni/Zn cell analyzed in Section 3.8, determine an I−V curve for the cell by solving for the current as a function of the voltage over the range from 1.0 to 2.2 V. Please comment on the shape of the resulting curve.

3.15. The following data are provided for the oxygen reduction reaction in acid media at 80 °C. The potential of the positive electrode, , is measured with respect to a hydrogen reference electrode, which in this case also serves as the counter electrode. Additionally, any ohmic resistance has been removed from the potentials tabulated.

1. Plot these data on a semi-log plot (potential versus log i). You may assume that the kinetics for the hydrogen reaction is fast, and thus the anode polarization is small. What is the Tafel slope (mV per decade) in the mid-current range?
2. Even though ohmic polarizations have been removed, at both low and high currents, the slope is not linear on the semi-log plot. Suggest reasons why this may be the case.

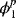
3.16. One common fuel cell type is the solid oxide fuel cell, which uses a solid oxygen conductor in place of an aqueous solution for the electrolyte. The two reactions are as follows:

I [A·m−2]	Vcell [V]
−6981	1.5006
−4871	1.3554
−2946	1.2074
−967	1.0549
930	0.9047
2799	0.7545
4753	0.6020
6836	0.4518
9328	0.3000

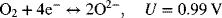
and at the positive electrode

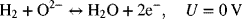
Data for the polarization of a solid-oxide fuel cell/electrolyzer are provided in the table. These potentials are the measured cell potentials, although the anodic overpotential is small and can be neglected. The temperature of operation is 973 K. The ohmic resistance of the cell is 0.067 Ω·cm². After removing ohmic polarization, how well can the reaction rate for oxygen be represented by a Butler–Volmer kinetic expression? Comment on the values obtained.

3.17. Using the data from Problem 3.3(b), calculate the current efficiency for the negative electrode of the lead–acid battery in the presence of the Sb impurity. A general rule of thumb is that the reaction rate doubles for each 10° increase in temperature. If the current density is held constant (use the value calculated at −0.44 V), what happens to the potential of the electrode and the current efficiency if the temperature is raised to 35 °C? You may neglect any changes in the equilibrium potential with temperature.

3.18. Referring back to Problem 3.1, when the potential of the electrode is changed away from 0.26 V, current will flow due to faradaic reactions. These reactions will continue until a new equilibrium is established. What is the effect of raising the electrode potential 10 mV above 0.26 V on the following:

1. The energy of an electron in the electrode?
2. During the period where the system is evolving to a new equilibrium, will oxidation or reduction take place?
3. What are the new values for the equilibrium concentration of ferri- and ferrocyanide?

CopycopyHighlighthighlightAdd NotenoteGet Linklink