In cases where migration can be neglected (e.g., excess supporting electrolyte), traditional methods and correlations for mass transfer can be used to determine reaction rates and the current density, which of course are related through Faraday’s law. In this section, we consider convective mass transfer for geometries that are of interest for electrochemical systems.

It is frequently convenient to describe mass transfer with a convective mass-transfer coefficient rather than molecular diffusion and a detailed description of the fluid motion. If, as mentioned previously, we restrict ourselves to cases where transport by convection is important and where migration can be neglected, we can use the multitude of correlations developed in other fields of engineering to describe mass and heat transfer. Generally, the flux is expressed as

(4.40)

where k_c is the mass-transfer coefficient with units of m·s⁻¹. Please note that although the flux is still a vector quantity, this quality has been lost with Equation 4.40. Therefore, you need to be careful to ensure that the sign is correct, and that transport is still from high concentration to low concentration. The difference in concentration between the bulk, c_i,bulk, and the surface, c_i,surf, is the driving force for transport.

Our interest in convective mass transfer is twofold. First there are a number of problems of interest where one needs to describe transport of reactants/products to or from the surface. Second, one can use electrochemical methods as a means of measuring mass-transfer coefficients and transport properties.

Typically, mass-transfer coefficients are correlated with dimensionless groups. A dimensional analysis of forced convection suggests that the Sherwood number is a function of the Reynolds and Schmidt numbers.

(4.41)

The three dimensionless quantities are

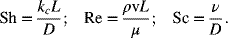
Note that the v in Re is the characteristic velocity. The Sh number is a dimensionless mass-transfer coefficient defined in terms of the characteristic length, L, and the diffusivity of the species being transported. For internal flow through a pipe or channel, the characteristic length is the diameter of the pipe or the hydraulic radius of the channel. Flow through an electrochemical cell is often represented as flow through a rectangular channel. For external flow such as flow over a flat plate or a cylinder, the characteristic length is the length of the plate or the diameter of the cylinder.

Unfortunately, dimensional analysis does not provide any help for the functional form of Equation 4.41. There are a number of cases from heat and mass transfer where analytical solutions are possible, but mostly the correlations of interest for electrochemical systems are empirical. Whether the result of analytical solution or experimental measurements, the correlations are of the form

(4.42)

where a and b are constants.

The definition of Sh can be combined with Equation 4.40 as follows:

(4.43)

It is sometimes advantageous to run an electrochemical cell at the limiting current. The mass-transfer limiting current represents the highest rate at which a cell can be operated and, therefore, the rate that maximizes production. At limiting current, Equation 4.43 becomes

(4.44)

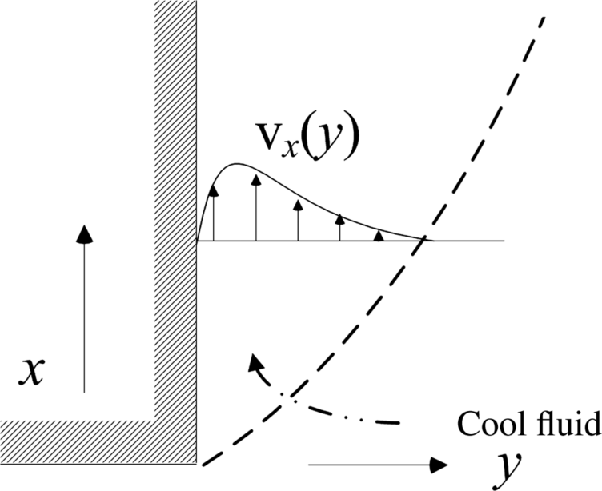
There are also important problems where the fluid motion is driven by density differences in the fluid rather than forced flow. Because of the gravitational field, buoyancy forces result from these differences in density. This effect is similar to flow induced by temperature differences, which is commonly studied in heat transfer and is called natural or free convection. As we saw earlier, electrochemical reactions often result in concentration gradients. These concentration differences can result in variations in density, which culminate in fluid flow. The boundary layer developed from a vertical electrode is sketched in Figure 4.8. For natural convection, the dimensionless mass-transfer coefficient is expressed as

(4.45)

where the Grashof number, Gr, replaces the Re number. The Grashof number is given by

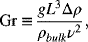
where g is the acceleration due to gravity, Δρ is the difference between the density of the bulk liquid and that at the surface of the electrode, ρ_bulk is the density of the bulk electrolyte and ν is the kinematic viscosity. The Re number is the ratio of inertial and viscous forces; similarly, the Gr number may be thought of as the ratio of buoyancy and viscous forces. The characteristic length for Gr is typically the height of a vertical plate or electrode, which is of particular interest to us.

For the most part, one can use these correlations without a comprehensive knowledge of their origin, which will be our approach here. The interested reader is directed to any number of texts that treat mass transfer in depth. Since these correlations are by and large empirical, it is important to know what characteristic length is used in the definition of Re, Sh, and Gr. Similarly, the velocity used in Re is essential. In contrast, Sc is a property of the fluid and thus independent of the flow.

The methodology of solving these convection problems will be illustrated by the following two examples. The first involves mass transfer in a parallel plate electrode; the second is an electrorefining example.

ILLUSTRATION 4.6

A divalent metal contaminant in water is removed by electrodeposition as it flows past parallel plate electrodes. The average velocity of the fluid is 0.05 m·s⁻¹, and the plate electrodes are separated by a distance of 1.5 cm and are 20 cm long. The counter electrode is located downstream of the working electrodes. Estimate the limiting current density. The concentration of contaminant is 0.1 M and its diffusivity is 7.1 × 10^-10 m²·s⁻¹. Use a density of 1000 kg·m⁻³ and a viscosity of 1 mPa.

Calculate the Reynolds number, . For the characteristic length, we use the hydraulic diameter, 

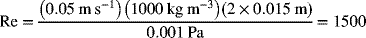
indicating laminar flow.

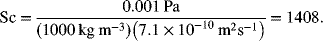
The following correlation for the Sherwood number is provided, assuming that the flow is laminar and well developed before reaching the electrodes. Since the electrodes are of finite length, there is an additional dimensionless parameter in the correlation that accounts for entrance effects, which are important in this problem.

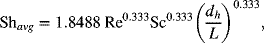
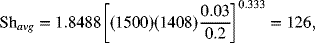
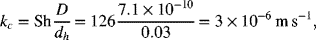
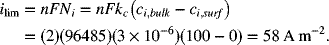
ILLUSTRATION 4.7

Copper is purified by a process known as electrorefining. Here Cu with some impurities is oxidized at one electrode and reduced at the other. The purity can be improved from 99 to 99.99% by this method. This is a huge operation—world production of copper is in the millions of metric tons per year.

The concentration of CuSO₄ is about 0.25 M and the supporting electrolyte is sulfuric acid with a concentration of about 1.5 M. Impurities more noble than Cu (see Appendix A), will not oxidize appreciably, and therefore do not enter the electrolyte. Metals, such as Ni that are less noble than Cu will not be reduced. Thus, if the potential is controlled carefully, the cathode can be significantly purer than the anode starting material.

Estimate the limiting current and the electrode area required to produce 1000 metric tons per day of copper. For a vertical electrode, free convection is assumed and the following correlation is suggested.

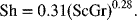
The following data are provided:

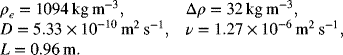
The Grashof and Schmidt numbers are calculated from the data provided:

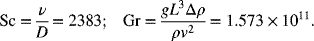
Next, the Sherwood number is estimated from the correlation; Sh = 3739.

The limiting current is when c_i = 0 at the surface. Therefore, 

Solving for i_lim = 100 A m⁻²,

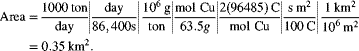
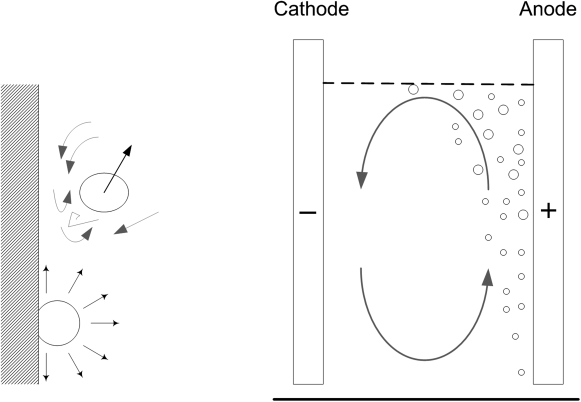
There are certain mass-transfer situations that are particularly relevant to electrochemical processes. For some systems gases are evolved on the electrode; for example, chlorine is evolved on the positive electrode in a chlor-alkali cell. Similar to boiling heat transfer, the bubbles disrupt the boundary layer near the electrode and dramatically enhance the rate of mass transfer. Additionally, the bubble can create macroscopic circulation of the electrolyte. Thus, as shown in Figure 4.9, gas evolution at one electrode may enhance mass transfer at the counter electrode.

To describe mass transfer at gas-evolving electrodes, the expansion of gas bubbles at the surface and its similarity to nucleate boiling was used as the basis of a correlation developed by Stephak and Vogt:

(4.46)

where the characteristic length in the Sherwood and Reynolds numbers is the break-off diameter of the bubbles. Measurements of the break-off diameter for hydrogen and oxygen evolution in both acidic and alkaline solutions yielded an average value of about 50 μm. This value of the diameter should be used unless more detailed information is available. Equation 4.46 was tested against a large number of experiments over a wide set of conditions involving hydrogen, oxygen, or chlorine evolution from acidic or alkaline electrolytes at temperatures ranging from 0 to 80 °C, and found to represent the data well in most cases. However, 15% of the data were found to lie outside an error margin spanning −50 to +100%, which is higher than the typical error found for correlations that do not involve formation of a second phase. The correlation found in Equation 4.46 is recommended for the calculation of mass-transfer rates at gas-evolving electrodes in the absence of experimental data for the specific system of interest.

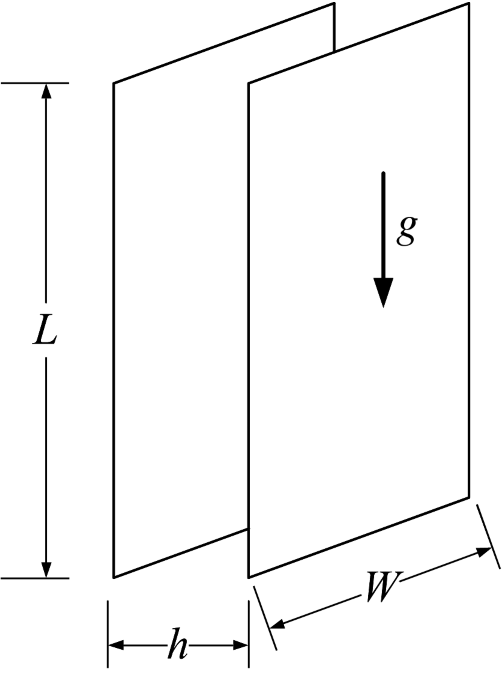
The above correlation is for the mass-transfer rate at the gas-evolving electrode itself. In addition, Mohanta and Fahidy¹ studied two vertical, parallel plate electrodes shown in Figure 4.10 where the evolution of gas at the anode affected the rate of mass transfer at the cathode. The gas flow will be upward, and the Reynolds number is based on the hydraulic diameter (see Illustration 4.6) and the superficial velocity of the gas:

(4.47)

where  is the volumetric flow of gas in m³ s⁻¹. Therefore,

(4.48)

Fahidy et al. provided the following empirical correlation for mass transfer at the electrode opposite that of the gas-evolving electrode:

(4.49)

Sh_o is the Sherwood number in the absence of bubbles; thus, the second term on the right side is the increase in mass transfer due to the bubbles at the opposite electrode. These and other correlations should be used cautiously as many are based on a small set of data and have only a weak theoretical basis. Nonetheless, Equation 4.49, for example, is consistent with the expected behavior. Specifically, if the distance between electrodes, h, is reduced, then the superficial velocity and Re increase, resulting in a higher mass-transfer coefficient. Additionally, if L is the length from the bottom of the electrode, as L increases, the mass-transfer coefficient increases because the bubbles reach further across the electrode (Figure 4.9).

The void fraction of the gas, ε, is also referred to as the “gas holdup,” . The superficial velocity of the gas is defined as the volumetric flow rate of the gas divided by the cross-sectional area of flow:

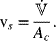
Often, the velocity of the gas relative to the velocity of the liquid can be determined. For example, the terminal velocity of a bubble in liquid for a diameter less than 0.7 mm is given by Stoke’s law:

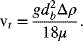
From the terminal velocity, the gas holdup can be estimated

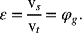
Finally, mass transfer can be improved by aggressively bubbling (sparging) a nonreacting gas through the electrolyte. This phenomenon is similar to natural circulation in that buoyancy forces are critical. Sigrist et al.² have proposed the following correlation:

(4.50)

The Archimedes number is similar to the Gr number, with the principal distinction being that in gas sparging there is a second phase present.

(4.51)

Ar characterizes the buoyancy and viscous forces on the bubble.

Rather than a single bubble, swarms of bubbles would be used to enhance mass transfer. In this case, the fraction of the volume occupied by the bubbles, ε, is important. Assuming that the density of the gas is small compared to the density of the liquid, the Ar number is modified to

(4.52)

In the empirical data, no dependence between the mass-transfer coefficient and either the height of the electrode, L, or the space between electrodes, h, was observed. Therefore, the correlation given by Equation 4.50 uses the bubble diameter, d_b, as the characteristic length in the Sh and Ar^*. As above, assume a bubble diameter in the electrolyte of 50 μm, unless additional information is given.