The Daniell cell that was examined previously presupposed a selectively permeable membrane separator. In practice, simple porous media are often used. In this case, bulk mixing is avoided, but ions are able to move between electrodes. In fact, we often have electrochemical cells where the two electrodes are in solutions of different concentration and/or composition. The thermodynamic analysis described above accounts for the effect of the local solution composition on the equilibrium potential. However, there is also a small potential difference at open circuit associated with the junction between the two liquids of different composition. This potential difference is sometimes called the liquid junction potential, and is the topic of this section.
The liquid junction of interest is the region of varying composition between the two different electrolyte solutions. In practice, it is often a porous membrane that inhibits mixing of the two solutions, although several other physical possibilities exist such as use of a capillary tube to form a stable liquid junction. Ions must be able to move through the junction in order for current to flow in the electrochemical cell since ions are the current carriers. However, under the open-circuit conditions discussed in this chapter, the current is zero. Under such conditions, diffusion can still take place, but there can be no net transfer of charge. This situation violates two tenets of our thermodynamic analysis. The first is that the system is at true equilibrium—with concentration gradients and transport this condition is not strictly met. The second assumption is that at least one species is absent from each electrode. This condition too can no longer be guaranteed.
With this brief background, we can now describe the origin of the liquid junction potential. For illustration purposes, we can consider the situation where we have different concentrations of the same 1 : 1 binary electrolyte on opposite sides of a porous membrane as shown in Figure 2.3. At open circuit, there will be a diffusion driving force for ions to move from the high concentration side to the low concentration side. The problem is that the cation and anion typically have different diffusion coefficients. The ion with the largest diffusivity will initially move faster than the counterion. This difference in velocity causes a slight imbalance of charge, which results in a potential difference across the junction. The associated potential field in the junction serves to slow down the faster ion and speed up the slower ion so they move at the same rate. This potential difference is the liquid junction potential.
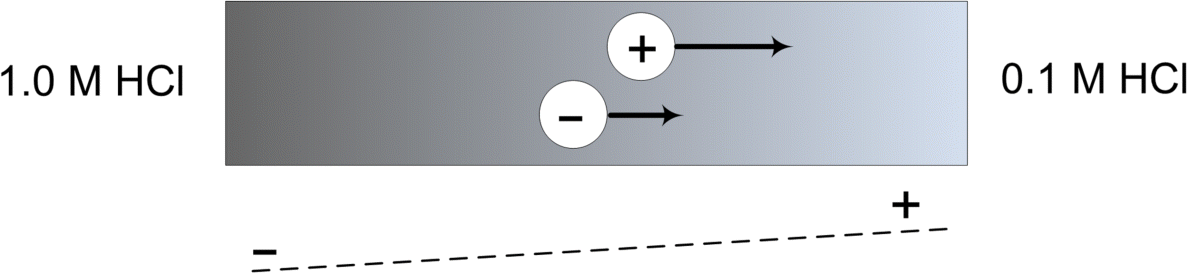
As you may have noticed from the above description, the liquid junction potential is the result of transport and is not thermodynamic in origin. The magnitude of this potential ranges from less than a millivolt to a few tens of millivolts (e.g., 20–30 mV), so that it is not a large correction. Hence, for the most part we will ignore it. Several methods exist for estimating the liquid junction potential. In general, the potential of a cell with a liquid junction can only be calculated with detailed knowledge of the concentration profile across the junction region. However, simplified methods such as the Henderson equation provide a common and straightforward way to estimate this potential. Awareness of potential errors from the junction potential may be important in selecting a reference electrode and in correcting measurements. Please refer to references in the “Further Reading” section for additional information.
There is one other aspect that is worth noting. Since the liquid junction potential is the result of the different transport rates of the anions and cations, the magnitude of this potential can be minimized by choosing anions and cations with similar diffusivities. Consequently, KCl is frequently used to minimize the junction potential. Finally, while we have described the situation for a binary electrolyte, the same physics and principles apply to multicomponent junctions.
Leave a Reply