At open circuit, no current flows between the electrodes. Furthermore, for our thermodynamic analysis, each electrode half-cell reaction is at equilibrium (no net anodic or cathodic reaction occurs at either electrode). Under these conditions, it is appropriate to write the half-cell reactions as reversible reactions. Since electrons are participants in each of the two reactions, the energy of the electrons in each conductor is determined by the reaction equilibrium at that electrode, and the electrical potential is different for each electrode. The difference in energy of the electrons at the two electrodes can be easily measured with a voltmeter as a voltage or potential difference. That potential difference at equilibrium is the principal topic of this chapter. This potential is also called the thermodynamic potential, U, since the half-cell reactions are at equilibrium.
Before proceeding with the analysis of electrochemical systems, it is productive to consider a simple, chemical-reacting system. A common exercise is to determine whether a reaction will occur spontaneously.
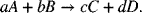
The criterion used is the sign of the change in Gibbs energy for the reaction as written, namely,
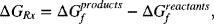
where ΔGf is the Gibbs energy of formation of the compound. If the change in Gibbs energy of the reaction, ΔGRx, is less than zero, then the reaction is said to proceed spontaneously. The first thing to note is that the sign of the change in Gibbs energy for the reaction depends on how the reaction is written, more specifically what is considered a product and what is treated as a reactant. Thus, it is more precise to say that the reaction will occur spontaneously as written. If the reaction is spontaneous, then we can obtain work from the reaction. If it is not spontaneous as written, then we would need to add work to force the reaction to go in that direction.
You are undoubtedly familiar with the reaction of hydrogen and oxygen, which combust to form water.
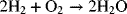
Using values from Appendix C for the Gibbs energy of formation for the reactants and products at their standard states, a large negative ΔGRx is calculated. Thus, we conclude that the reaction as written will occur spontaneously, which is consistent with our expectations. Now of course, pure hydrogen and oxygen present together at near atmospheric pressure doesn’t sound like the true thermodynamic equilibrium we seek. In fact, if these three species were together in equilibrium, we would find almost all water and only trace amounts of oxygen and hydrogen gas in our system. At this equilibrium state, the reactants and products are far from their standard states, and the change in Gibbs energy would be zero.
A hallmark of equilibrium of electrochemical systems is that there are two electrodes and at least one of the species is absent from each electrode. Furthermore, as noted earlier, electrons are involved in the half-cell reactions and, while the circuit is open, no electrons can be transferred between the two electrodes. Therefore, the half-cell reaction at each electrode will reach a dynamic equilibrium involving electrons where the rates of the forward and reverse reactions at that electrode are equal and there is no net current. The energy of the electrons for each of the half-cell reactions at equilibrium is different; this difference in electron energy, characterized by the potential difference, is what drives the full-cell reaction when the circuit is closed.
The same overall reaction of hydrogen and oxygen described above can occur electrochemically with two half-cell reactions. For instance,
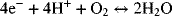
and
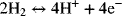
Notably, hydrogen is absent from the oxygen electrode, and oxygen is missing from the hydrogen electrode. At open circuit (i.e., no external current flow, and allowing sufficient time for equilibrium to be established), we can use thermodynamics to develop a relationship between the equilibrium cell potential, U, and the thermodynamic state of the reactants and products. In contrast to the combustion situation, it is possible for equilibrium to exist with significant amounts of hydrogen, oxygen, and water all present in the same electrochemical cell. This is because the hydrogen and oxygen are separated, with the hydrogen reaction in equilibrium at one electrode and the oxygen reaction in equilibrium at the other. In fact, we can now vary the amount of hydrogen, oxygen, and water independent of each other. However, the equilibrium potential of the cell, U, changes, and it is precisely this change in potential that is of interest here.
The laws of thermodynamics for a closed reversible system at constant temperature and pressure tell us that the maximum work that can be done by the system on the surroundings is equal to the change in the Gibbs energy per mol, ΔG [J·mol−1]. In the electrochemical system of interest, that work is electrical work. In other words,
where work done by the system on the surroundings is defined as positive.
The cell potential, U, has units of joules per coulomb (J·C−1, which is also V) and represents the work per unit charge required to move charge from one electrode to the other. The amount of charge transferred in the full reaction is equal to nF, where n is the number of moles of electrons in the reaction as written, and F is Faraday’s constant, the number of coulombs per mole of electrons. The electrical work is therefore
Combining (Equations 2.1) and (2.2) yields
Equation 2.3 applies to a full cell consisting of an anodic and cathodic reaction, and relates the change in Gibbs energy for the chemical species to the difference in the electron energy at the two electrodes. Generally, we treat the potential of a full cell, U, as the potential difference between the more positive electrode and the more negative electrode. When this is done, U is positive and ΔG is negative for a full electrochemical cell at equilibrium. As described previously, a negative change in Gibbs energy implies a spontaneous reaction. This is in fact correct; when the circuit is closed for any cell at equilibrium that has a nonzero potential, current flows spontaneously. In order to ascertain the reactions that are occurring and the direction of the current, we simply choose the direction of the reaction such that the change in Gibbs energy is negative. In our example with hydrogen and oxygen, writing the reaction as
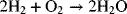
resulted in a negative change in Gibbs energy, indicating that at one electrode hydrogen is oxidized (anode), and at the other electrode oxygen is reduced (cathode) to produce water when the circuit is closed. We now turn our attention to calculating the equilibrium potential of cells before the circuit is completed; i.e., at open circuit.
Leave a Reply