Wertheim’s Theory of Polymerization

Now that we have an accounting for the thermodynamics of bond formation, it is natural to wonder what happens to the thermodynamics as the bond energy approaches infinity. This would be a natural limit for covalent bond formation. Having a theoretical basis for nonspherical molecules would be a big step forward, considering that all theories discussed until now have been based on spherical molecules. Of course, we added correction terms like α(T, ω) to the Peng-Robinson model, but this was done with no theoretical basis. Wertheim’s theory provides an opportunity to develop meaningful guidelines for shape effects.

The key step is to find the contribution to the equation of state from forming a bond in the limit of infinite bond energy. The result for binary association, Eqn. 19.54, is convenient to illustrate the key points. At first glance, the limit may not seem obvious, because the X term in A^chem must approach zero and the log term would then be undefined. This issue can be resolved by substituting, say, 1 – X = X²Δ. We use A^bond to denote the covalent nature of the bonds.

---

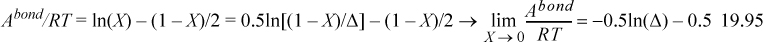
Example 19.6. Complex fugacity for the van der Waals model

A sample calculation with a specific reference equation of state should clarify these results. Let K₁₂^AD = K₂₂^AD = 0.72 cm³/mol and ε₁₂^AD = ε₂₂^AD = 20 kJ/mol, b₁=27.5 and b₂=20.4 cm3/mol.

a. Derive Z^chem and ln(φ_k^chem) adapting the definition of Δ from Eqn. 19.44.

b. Evaluate the expressions for trimethylamine(1) + methanol(2) at x₁ = 0.5, ρ = 0.0141mol/cm³, and T = 300K.

Solution

a. Δ_ij^AD = ρK^AD(exp(βε_ij^AD) – 1)/(1 – η_P) = Δ.

Eqn. 19.65 shows that ηP∂Δ/∂ηP = Δ/(1 – η_P)

Substituting gives Z^chem = –0.5h/(1 – η_P). For ln(φ_k^chem) Eqn. 19.93 requires n∂(Δ_ij^AD/n)/∂n_k, 

Similarly, n∂(Δ_ij^DA/n)/∂n_k = (Δ_ij^DAb_kρ)/(1 – η). Substituting this result into Eqn. 19.93 gives,

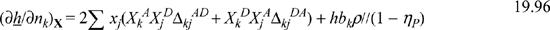
b. Evaluating these expressions, Δ₁₁^DA = Δ₁₂^DA= 0 because trimethylamine (TMA) has no donors, so X₁^D = 1. It may seem odd to represent X₁^D = 1 when there are no donors, but site occupation is impossible when Δ = 0 for that site.

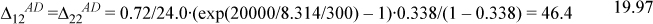
To solve Eqns. 19.93 for X₁^A, X₂^A, and X₂^D,

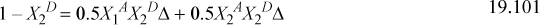
This gives three equations. Rearranging (below) shows that X₁^A = X₂^A. We can replace these to obtain a quadratic equation in terms of X₂^D. Usually, we would need to iterate to solve for X₂^D.

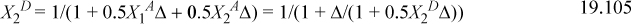
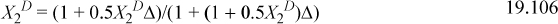
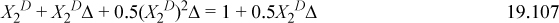
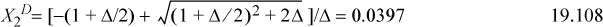
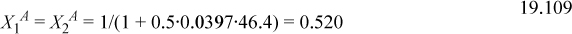
This shows that X₂^D is almost completely bonded.

By Eqn. 19.88,

h = x₁²X₁^AX₁^DΔ₁₁^AD + 2x₁x₂X₁^AX₂^DΔ₁₂^AD + x₂²X₂^AX₂^DΔ₂₂^AD + x₁²X₁^DX₁^AΔ₁₁^DA + 2x₁x₂X1^DX₂^AΔ₁₂^DA + x₂²X₂^DX₂^AΔ₂₂^DA

Substituting x₁, x₂, and X gives

h = 0 + 2·x₁x₂·X₁^AX₂^D·46.4 + x₂²X₂^AX₂^D·46.4 + 0 + 0 + x₂²X₂^DX₂^A·46.4 = 0.960
Z^chem = –0.5h/(1 – η_P) = –0.480/(1 – 0.338) = –0.725

By Eqn. 19.92,

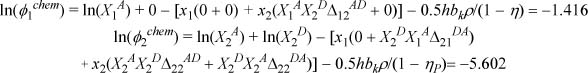
There are several points of interest in this result. The acceptors in this mixture outnumber donors by two to one. Therefore, it is impossible that X_i^A< 0.5, and, in fact, X₂^D ~ 2·(X₁^A – 0.5) because the lack of donor saturation is reflected twice, in X₁^A and X₂^A. The compressibility factor is depressed in a simple way that sums over all donors and acceptors, but the fugacity is depressed more for the alcohol than for the amine. There are three ways for the alcohol to interact, but only one for the amine, so the depression of the fugacity is much greater. On the other hand, the fugacity of the alcohol is depressed less in the mixture than in the pure fluid because relatively fewer acceptors are bonded (ln(φ₂^chem)= –6.105 at x₂ = 1). So the activity of the alcohol in the mixture is relatively enhanced by hydrogen bonding while the activity of the amine is depressed at all compositions.

---

---

Example 19.7. More complex fugacity for the van der Waals model

Evaluate the expressions for Z^chem and ln(φ_k^chem) of trimethylamine(1) + methanol(2) at x₁ = 0.4, ρ = 0.0141 mol/cm³, and T = 300 K. Let K₁₂^AD = K₂₂^AD = 0.72 cm³/mol and 1.25ε₁₂^AD = ε₂₂^AD = 20 kJ/mol, b₁ = 27.5, and b₂ = 20.4 cm³/mol.

Solution

The difference between this example and the previous is that ε₁₂^AD ≠ ε₂₂^AD, indicating that the solvation is slightly weaker than the alcohol association. Because of this lack of symmetry, an iterative solution for X is required. Recalling part (a) of the previous example,

Z^chem = –0.5h/(1 – η_P)

For ln(φ_k^chem): –∑ x_j(X_k^A X_j^DΔ_kj^AD + X_k^DX_j^A Δ_kj^DA) – 0.5hb_kρ/(1 – η_P)

Substituting the mole fractions and solving for Δ’s,

b = 0.4·27.5 + 0.6·20.4 = 23.4; η_P = 0.0141·23.4 = 0.328. This is slightly less than Eqn 19.99.

Δ₂₂^AD = ρK^AD(exp(βε₂₂^AD) – 1)/(1 – η) = 45.8. Δ₁₂^AD = 9.21; Δ₁₁^DA = Δ₁₂^DA = 0.

1 – X₁^A = 0.5X₁^AX₂^DΔ₁₂^AD; 1 – X₂^D = 0.5X₁^AX₂^DΔ₁₂^AD + 0.5X₂^AX₂^DΔ₂₂^AD;

1 – X₂^A = 0.5X₂^AX₂^DΔ₂₂^AD;

X₁^A = 1/(1 + 0.4X₂^DΔ₁₂^AD); X₂^A = 1/(1 + 0.6X₂^DΔ₂₂^AD);

X₂^D = 1/(1 + 0.4X₁^AΔ₁₂^AD + 0.6X₂^AΔ₂₂^AD);

Unlike the previous example, an explicit solution is not found. The previous example was contrived to achieve an exact solution, but this is rarely possible. Normally, we must iterate to achieve a numerical solution. It is convenient to guess X₂^D, then compute X₁^A and X₂^A, then check the new value of X₂^D based on X₁^A and X₂^A. To initialize X₂^D, a reasonable estimate can be based on a variation of the solution for Δ_kj^AD =(Δ_kk^ADΔ_jj^AD)^1/2.

Applying Eqn. 19.94,

(–1 + 1/X₂^D) ≈ Σ x_jΔ_2j^AD/[1 + (Δ_jj^AD)^1/2] = 0.122 ⇒ X₁^A = 0.597; X₂^A = 0.230; X₂^D = 0.105;

Five more iterations give, X₁^A = 0.678; X₂^A = 0.297; X₂^D = 0.0855. Five iterations is actually a large number because this particular mixture deviates substantially from the SRCR.

X₁^A = 1/(1 + 0.4·0.0857·9.21)= 0.678

X₂^A = 1/(1 + 0.6·0.0857·45.8)= 0.297

X₂^D = 1/(1 + 0.4·0.678·9.21 + 0.6·0.297·45.8) = 0.0855

Substituting into Eqn. 19.88

h = x₁²X₁^AX₁^DΔ₁₁^AD + 2x₁x₂X₁^AX₂^DΔ₁₂^AD + x₂²X₂^AX₂^DΔ₂₂^AD

+ x₁²X₁^DX₁^AΔ₁₁^DA + 2x₁x₂X₁^DX₂^AΔ₁₂^DA + x₂²X₂^DX₂^AΔ₂₂^DA

h = 0 + 2·x₁x₂·X₁^AX₂^D·9.21 + x₂²X₂^AX₂^D·45.8 + 0 + 0 + x₂²X₂^DX₂^A·45.8 = 1.097

Z^chem = –0.5h/(1 – η_P) = –0.480/(1 – 0.328) = –0.816

ln(φ₁^chem) = ln(X₁^A) – [x₁(0 + 0) + x₂(X₁^AX₂^DΔ₁₂^AD + 0)] – 0.5hb_kρ/(1 – η_P) = –2.228

ln(φ₂^chem) = ln(X₂^A) + ln(X₂^D) – [x₁(0 + X₂^DX₁^AΔ₂₁^DA)

+ x₂(X₂^AX₂^DΔ₂₂^AD + X₂^DX₂^AΔ₂₂^DA)] – 0.5hb_kρ/(1 – η_P) = –5.855

These results show that a 20% change in ε₁₂^AD compared to Example 19.6 gives a 500% change in Δ₁₂^AD. That is fairly sensitive. This change in Δ₁₂^AD is primarily responsible for the increase in X₁^A from 0.520 to 0.679 and the decrease of X₂^A from 0.520 to 0.298. Overall, the chemical contributions are slightly stronger because the composition of amine has been reduced.

---

Eqn. 19.95 is helpful when Δ→∞ because Z can be obtained by differentiation of A. Taking the derivative,

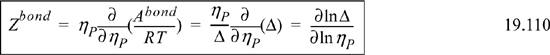
From a model for Δ, the bonding contribution to the EOS results. For example, if Δ is given by the van der Waals model,

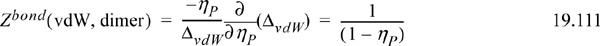
Generalizing this result to a chain with m segments, there are (m–1) bonds per chain. For example, continuing with the vdW model,

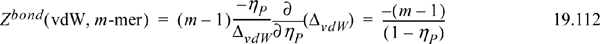
This is essentially Wertheim’s theory of polymerization, although Wertheim specifically treated the case resulting in a mixture with a range of molecular weights and average degree of polymerization of <m>.²²