The general approach is exactly what you would expect: Write all the reaction and phase equilibrium constraints and then solve the nonlinear system of equations. Making this approach into a practical alternative to, say, the Peng-Robinson model requires several clever observations, approximations, and rearrangements, however. Wertheim’s theory is based on the contribution to the Helmholtz energy. In the end, Achem is recognizable as a distinct contribution with a firm foundation in experimental observation and molecular simulation that adds just one intermediate (but robust) step in solving for the density given temperature and pressure.
Wertheim’s theory has the same objective as this chapter: to develop a theory for the chemical contribution to the Helmholtz energy, Achem, and consequently Zchem, through the derivative relations in Chapter 6. Because the volume derivative of A results in P, the volume (or density) derivative of A can be used to calculate the contribution of chemical interactions to Z. Wertheim’s theory refers to the concepts of monomers and dimers discussed previously, but develops a self-contained and self-consistent model based on a given equation of state for the nonchemical contributions. In Chapter 7, we demonstrated that an equation of state expression for Z could be written in terms of the repulsive Zrep and attractive Zatt contributions. (i.e., Arep and Aatt, aka the “physical” contributions). Wertheim’s original development uses sophisticated statistical mechanics beyond the scope of this introduction. Nevertheless, we can understand his results in terms of contributions to the reaction and equilibrium equations. Whenever we arrive at a set of terms that seems difficult to simplify, we can apply Wertheim’s result as a “clever guess,” and show how this result leads to a self-consistent interpretation for specific physical contributions (e.g., the van der Waals model). Once we have an expression for Achem expressed in terms of ρ0 and T, it can be added to the physical contributions and the equation of state can be applied like any other equation of state.
Because the notation is complicated, we develop this section using pure components, and later generalize the results. Wertheim’s theory is applied to equations of state, so we use the notation x to represent mole fractions in both the vapor and liquid phases and the state of aggregation will be determined by the size of Z. Also, we omit the “A” from xAM when there is only one component. The starting point for Wertheim’s theory is to rearrange the analysis in terms of the true numbers of bonding sites in the fluid. The extent of association is then characterized in terms of the fraction of bonding sites not bonded:

This “fraction of bonding sites not bonded” is closely related to the fraction monomer, xM. The relevant mass balances are discussed below. To understand Wertheim’s theory, you must understand what is meant by a hydrogen bonding site. A key element of Wertheim’s perspective is to characterize the bonding sites as small, off-center “blisters” of attractive energy. This gives orientational specificity because the sites can only bond if the angle from the left repulsive site to the bonding sites to the right repulsive site is close to 180°; any other orientation would be inconsequential. Furthermore, the smallness of the blister relative to the repulsive site means that three sites cannot bond simultaneously because it would require the third repulsive to overlap with the two that were already bound as shown in Fig. 19.6. This captures the short-range nature, orientational specificity, and steric hindrance that we recognize in hydrogen bonding, and complexation in general.
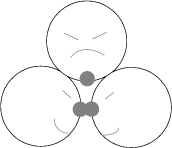
Figure 19.6. Wertheim’s perspective on bonding sites. The shaded portions represent the blisters. The lower two molecules are happily bonded, but the upper molecule can’t join the same bond.
Dimer Formation
We begin with association to form a dimer. For the formation of a dimer (denoted with subscript D), Eqn. 19.4 and the sum of true mole fractions can be combined and rearranged to relate the apparent moles n0 and total true moles nT to the fraction of unbonded sites X:
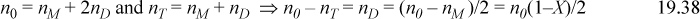
Dividing Eqn. 19.38 by n0 gives 1 – nT/n0 = (1 – X)/2, where X is the fraction of bonding sites not bonded:

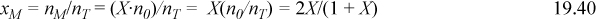
Noting that the solution must satisfy the mass balance, Eqn. 19.20, xM + xD = 1. Together with the reaction equilibrium (law of mass action, Eqn. 19.34) we may write,
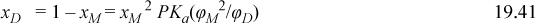
Substituting Eqn. 19.40 gives 1 – 2X/(1 + X) = 4X2PKa(φM2/φD)/(1 + X)2, which can be rearranged to
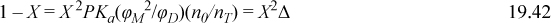
Defining

may seem odd at first glance, but it is one of the major simplifications derived from Wertheim’s theory. We outline his analysis below, but a key step was when Wertheim showed that this conglomeration of symbols can be simplified to

where g(σ) is the radial distribution function at contact distance σ, εC is the bond energy of the complex, and KC is the bonding volume related to the size of the “blisters.”13 Eqn. 19.42 shows that X can be solved directly from the density and temperature since Δ is a function of ρ and T. Since the density and temperature must be specified in applying the physical contributions of the equation of state anyway, the interjection of this contribution does not complicate matters in the way that solving simultaneous phase and reaction equilibria does. Imagine how cumbersome this model might become if all complexation required iterative solution. The principles are the same, but the feasibility is radically altered.
Aside from the advanced statistical mechanical analysis of Wertheim’s paper, we can appreciate the phenomenology of his analysis in two ways. First, we can recognize Δ as an equilibrium constant of a reversible reaction, the ratio of forward and reverse rates. The forward reaction is proportional to the probability of the sites finding each other. This probability is zero if the density is zero, and it is enhanced by g(σ). The reverse reaction is inhibited by the strength of association. The stronger the bonding energy, the slower the dissociation.14 Second, we can apply the van der Waals model with some simple assumptions. If we assume that bD = 2bM, aDD = 4aMM, and aDM = 2aMM, we obtain a similar result, in the manner of Heidemann and Prausnitz as shown in Fig. 19.7. Applying these assumptions to the fugacity coefficients of the van der Waals equation and substituting into Eqn. 19.42, we obtain,
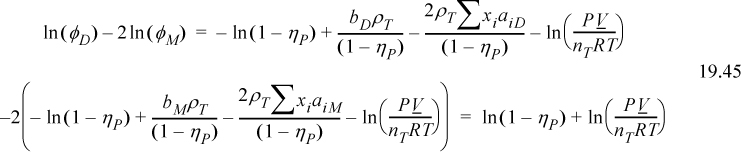
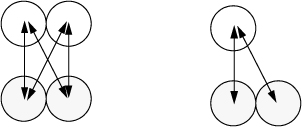
Figure 19.7. Illustration that aDD = 4 aMM and aDM = 2 aMM are reasonable by adding the number of pair interactions.
Simplifying gives,
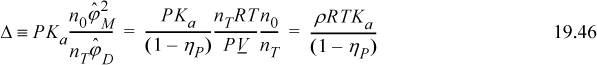
Note that the vdW EOS corresponds roughly to g(σ) = 1/(1 – ηP). Also, the equilibrium constant, Ka, can be referenced to the critical temperature and written as,
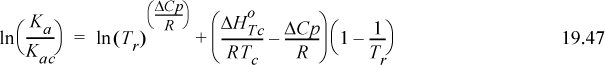
The “best” expression for ΔCp/R is debatable. Experimental measurements are unlikely to provide sufficient precision to resolve the debate. From a practical perspective, we would prefer a compact expression for Ka. From a theoretical perspective, Wertheim’s analysis is the most sophisticated. Suresh and Elliott15 used Tc as a reference temperature, and showed that Wertheim’s analysis is consistent with the assumption that,
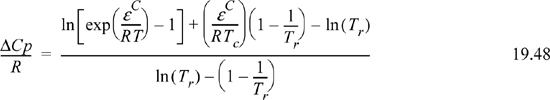
Substitution shows the resulting relation between Ka and a portion of Eqn. 19.44,
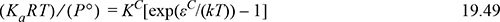
where (KacRTc)/(P°) = KC and –ΔHTc / R = εC / k. The superscript “C” denotes a C-type association but the relations can be extended to an AD-type (though an arbitrary reference temperature must be selected for AD interactions).16 Substituting this expression for Ka in 19.46 and g(σ) for 1/(1 – ηP) results in Eqn.Eqn. 19.44, eliminating the need to solve iteratively for the density, monomer and dimer concentrations, and fugacity coefficient ratio. An additional step is required to transform the extent of reaction (implicit in X) into a remarkably simple thermodynamic contribution, Achem.
Low Density
The next objective is to evaluate the impact on Helmholtz energy, Achem, the change in Helmholtz energy due to bonding. As discussed in the introduction, Achem is the chemical contribution as it pertains to an equation of state. Let’s begin by rewriting the Gibbs energy for a single bond at low density, noting that PV = nTRT then.17
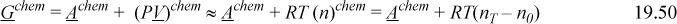
Or, on a apparent molar basis, (dividing by n0),

In rearranging, note that Gchem = Δμchem = RT ln ![]() , where
, where ![]() is the total fugacity with association fully recognized and f0 is the apparent fugacity based on zero association.
is the total fugacity with association fully recognized and f0 is the apparent fugacity based on zero association.
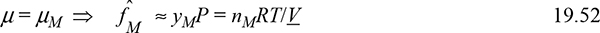
Further noting that
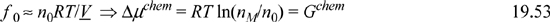
Substituting Eqns. 19.39 and 19.53 into Eqn. 19.51, and recalling X = nM/n0, we have

This turns out to be a very powerful equation.
All Densities
The remarkable aspect of Eqn. 19.54 is that it is accurate for all densities and extents of association, although it has been derived here only for binary association at low density. In fact, the significance of Wertheim’s work is that he provides a rigorous statistical mechanical derivation of this identity at all conditions. Once again, we can support this result phenomenologically through the van der Waals model. Adapting Eqn. 19.38,
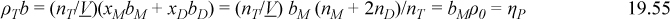
This equation shows that there is no overlap of repulsive sites when a hydrogen bond occurs, so the volume occupied by molecules is the same regardless of association. Similarly,
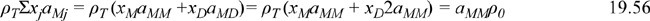
We can express the fugacity of the fluid in two ways, noting that fM = f where fM is defined by the monomer fugacity in the mixture, that is, ln(φM) = ln(fM/xMP), and f is defined by ln(f/P) = (G – Gig)/RT for the “pure” fluid based on the apparent perspective. The expression in terms of φM relates to the true species and uses the fugacity expression for a component in a mixture. The expression in terms of f/P emphasizes that we are still discussing a single pure component,
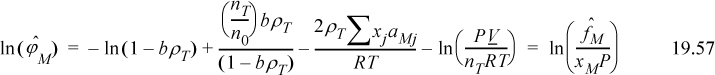
By Eqns. 19.55 to 19.56,
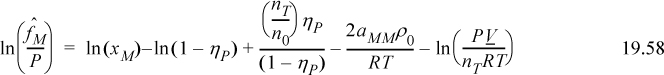
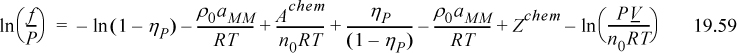
Equating 19.58 to 19.59, we can immediately cancel terms of ln(1 – ηP) and ρ0aMM. Also noting that ln(PV/n0RT) – ln(PV/nTRT) = ln(nT/n0),
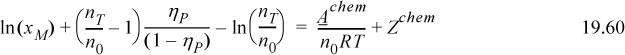
noting that xM·nT/n0 = X, and from Eqn. 19.39 (nT/n0 = (1+X)/2), we obtain,
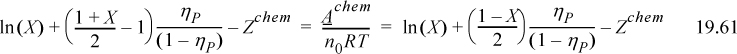
Recall that Z/ηP = d(A/RT)/dηP. Taking Eqn. 19.54 as a trial solution and checking that it is consistent with Eqn. 19.61,
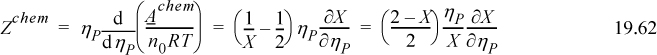
We can evaluate ∂X/∂ηP through Eqn. 19.42 by differentiating implicitly.
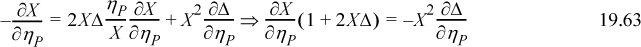
Multiplying and dividing the left side by X and replacing X2Δ with 1 – X, then multiplying and dividing the right side by Δ and replacing X2Δ with 1 – X, we obtain,
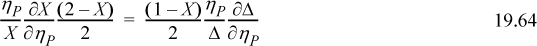
Recalling the definition of Δ from Eqn. 19.44,
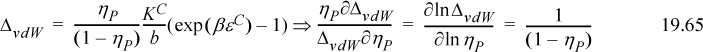
Substituting Zchem = (–1 + 1/X) / [2(1 – ηP)] gives
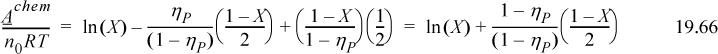
Hence we have recovered Eqn. 19.54 and verified our trial solution, using the van der Waals model, without the assumption of low density.The online chapter notes include a demonstrationthat Eqn. 19.54 is also recovered with the ESD model. Altogether, we can thoroughly appreciate the results of Wertheim’s analysis, even if the rigors of Wertheim’s statistical mechanics exceed our current scope. We can derive the framework of the simultaneous reaction and phase equilibria and see the crucial terms requiring simplification. At that point, Wertheim’s “clever guesses” provide a tremendous simplification of an immensely complex problem, all the more remarkable when recognizing that they are thoroughly grounded in a rigorous fundamental analysis.
Given Eqn. 19.54 for the free energy and Eqn. 19.42 to solve for X, the problem is essentially solved. Z = 1 + Zrep + Zatt + Zchem can be solved at a given T and P by iterating on ρ. Then the free energy equation yields the fugacity. The algorithm to solve for apparent density is illustrated in Fig. 19.8. Relative to the numerical solution of binary association in a pure fluid, this result might not seem so impressive. Nevertheless, further analysis shows that the extension to chain association of multiple components requires the same effort from Wertheim’s perspective, whereas the numerical solution quickly becomes overwhelming.
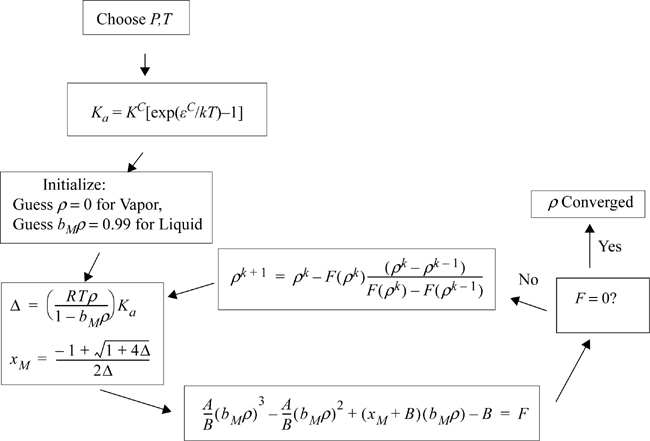
Figure 19.8. Flow sheet for calculating density by the van der Waals associating fluid model.
Example 19.4. The chemical contribution to the equation of state
Assuming Δ is about 1000 at 300 K and ρ = 1.04 g/cm3, estimate Achem/RT, Zchem, and xM of liquid acetic acid. You may assume that bM = 23 cm3/mol and the van der Waals model for Z.
Solution
Referring to Eqn. 19.66, Achem/RT = ln(X) + (1 – X)/2 and Zchem = –(1 – X) / [2(1 – ηP)]
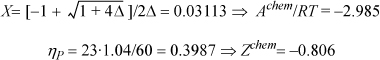
Referring to Eqn. 19.39, xM = 2X/(1 + X) = 0.06037
Comparing xM to X, the true solution is 94% dimer and 97% of the acid molecules exist in the dimer form. It is also interesting that Zchem < –0.5 for this liquid phase. The amount of dimerization would decrease at lower density, and for the gas phase it would be significantly lower, with Zchem smaller in magnitude.
Chain Association
To extend the analysis from dimer formation to model chain formation, the primary adjustment is to assign two sites per molecule, consistent with one proton acceptor (A) and one proton donor (D), as we might expect for an alcohol. We can easily count the number of acceptors and donors in such linear chains by noting that one unbonded acceptor is left in each bonded chain, referring to Fig. 19.9. The equations for donors are entirely symmetrical and are omitted for simplicity. Note that nA (the mole number of acceptors not bonded) is something quite different from nA (the mole number of an “A-mer”). The extent of association is then characterized in terms of the fraction of acceptor sites not bonded, XjA. To see the relationship, consider the mass balances We obtain,

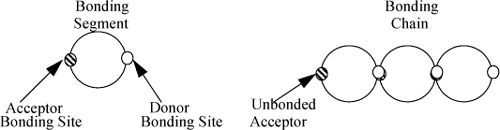
Figure 19.9. Wertheim’s theory of chain association in a two-site model.
But the total number of acceptors is given by noting that there are “j” total acceptors per j-mer,

Note that no refers to the same apparent number of moles discussed previously. Therefore,

There is a further simplification that results from treating the bonding sites instead of the bonding molecules. The fraction of sites bonded can be perceived as a simple product of the bonding probabilities. First, note that the fraction of monomers bonded, xAD, and the fraction of monomers not bonded, XA, must sum to unity.

xAD is the fraction of acceptors that are bonded, regardless of whether they are bonded in monomers, dimers, trimers, … In principle, the second term is an infinite sum. From an acceptor site perspective, however, we assume that the thermodynamic change from the unbonded state to the bonded state is the same, regardless of the degree of polymerization for that i-mer. That is, adding one more monomer to the end of a chain has the same equilibrium constant regardless of the chain length. Chemically, we have
That transition can be represented by

where XD is the fraction of unbonded donors and ΔAD = ρg(σ) KAD[exp(εAD/kT) – 1] adapts Eqn. 19.44 to AD interactions. The term on the left is the fraction of acceptors that are bonded, and the term on the right expresses the observation that acceptors and donors must be unbonded in order to be available for bonding. By noting that one donor bonds for every acceptor, we see that XA = XD. Then we write Eqn. 19.72 in terms of XA, (XA)2, and ΔAD and we can solve the quadratic equation to obtain

The extension of the Helmholtz energy to chain formation simply applies the same formula developed for dimer formation. This formula accounts for the change in entropy and energy each time a bond is formed. Whether the bond is formed as part of a dimer or part of a chain, the reduction in entropy by forming a bond is the same. So is the energy released by the bond formation. In terms of acceptors and donors for a pure fluid, Eqn. 19.54 becomes,
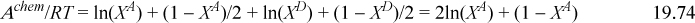
Eqns. 19.73, 19.74, and 19.44 characterize the chemical contribution for molecules like alcohols. Given a temperature and density, Eqn. 19.44 gives ΔAD, then Eqn. 19.73 gives XA, then Eqn. 19.74 gives A chem, then Eqn. 19.1 gives (A – Aig). Altogether, just one extra step (Eqn. 19.73) is required to compute the Helmholtz energy relative to the van der Waals model, but the rigor of the chemical perspective is greatly enhanced. In the MOSCED model, for example, the contribution involving (αi – αj)(βi – βj) is entirely empirical. It is contrived to give the right sign when mixing acids and bases, but there is no basis for it in theory, and it does not alter the skewness of the excess Gibbs energy. On the other hand, Wertheim’s theory is based on a rigorous derivation relating the molecular scale bonding volume and energy to the macroscopic properties, and fundamentally altering the behavior of the Gibbs energy.
Extension to Mixtures
Analyzing the impact of the chemical contribution on excess Gibbs energy requires extension of Wertheim’s theory to mixtures. The beauty of Wertheim’s perspective is that the extension of the reaction equilibrium relation (Eqn. 19.72) is entirely straightforward. One donor must bond for each bonded acceptor, whether the molecules are mixed or pure. The only issue is which molecule possesses the acceptor and which possesses the donor, but that is a notational detail. Furthermore, the fraction of bonded acceptors on the ith molecule must be in equilibrium with the unbonded donors and acceptors. The only difference is that the transition of an acceptor to being bonded can be effected by any donors, including those on other molecules. We simply need to sum all the transition probabilities and the extension becomes:

where xi is the apparent mole fraction of component i and Nd,i is the number of hydrogen bonding segments in component i. Nd,i accounts for the prospect that one molecule could have several donors, like the hydroxyl sites in polyvinyl alcohol. The extension of Eqn. 19.44 to mixtures becomes
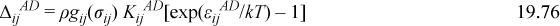
The ordering of the subscripts and superscripts in Eqn. 19.76 provides the notational detail that permits accounting for which bonding site resides on which molecule. For example, by writing εijAD, it is implied that the acceptor is on the ith component and the donor is on the jth. To designate the energy of a donor on the ith component with an acceptor on the jth, we should write εijDA. To clarify, this distinction might be important in a mixture of alcohols (i) and amines (j), for example. An amine is usually a weak proton donor (indicated by its low acidity, αj) but a strong proton acceptor (indicated by its basicity, βj), whereas a typical alcohol has roughly equal acidity and basicity (αi = βi). If we suppose that βi ~ βj, then εiiAD ~ εijAD > εijDA ~ εjjDA. This would mean strong solvation for the amines and negative deviations from Raoult’s law, as observed experimentally. Eqns. 19.75 simply states that the bonding probability for an acceptor on the ith species increases when there are donors on other molecules, and it decreases proportional to the mole fraction when the donor species are diluted by nonassociating species. The precise extent of chemical interaction is controlled by ΔijAD, which could range from zero (for alkanes in water, for example) to a substantial quantity (when mixing carboxylic acids, for example).
The extension of Achem to any number of bonding sites or components becomes,
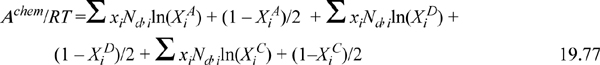
Briefly, this equation indicates that the change in Helmholtz energy due to bonding is the same regardless of how those bonds are formed. In other words, the reduction in entropy due to bond formation is universal when the packing fraction is unchanged. We know that entropy is the primary contribution because energy does not appear explicitly in Eqn. 19.77. Bonding energy affects Achem implicitly through Δ, because a larger energy gives a larger value of Δ and a smaller value of XiB. We have included XC here to represent dimerization (e.g., carboxylic acid bonding) as something distinct from AD interaction. A’s can only bond with D’s, and this leads to chain formation. On the other hand, C’s can only bond with C’s, confining these sites to dimerization. Although we wrote the equation for these three types of bonds, there is really no limit and Eqn. 19.77 can be extended straightforwardly to many situations. In the description here, XC would not affect XA because C’s can only interact with C’s. If a carboxylic acid (e.g., acetic acid) is to interact with an alcohol (e.g., water), A’s or D’s would need to be included as part of the carboxylic acid segment, in addition to the C’s, as illustrated in Fig. 19.10.18
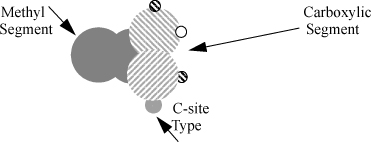
Figure 19.10. A bonding site model for acetic acid.
Eqns. 19.75–19.77 provide a powerful and versatile complement to our treatment of phase equilibria. In Chapters 10–12, we might have alluded to hydrogen bonding, for example, as a reason why oil and water do not mix, but our models did not truly recognize it as bonding. The van der Waals models and local composition theories treat attractive energy as spherically symmetric, like the square-well potential. But complexation is stereospecific and this alters the description of the Helmholtz energy. The Helmholtz energy of hydrogen bonding is as different from that of the van der Waals model as Eqn. 19.77 is from aρ/RT.
Leave a Reply