The transformed Gibbs energies in Section 18.12 are a convenient method to handle biological reactions but the details were not discussed earlier. The transformation of Gibbs energy to a field of buffered pH is analogous to the other Legendre transforms used previously. To obtain Gibbs energy from internal energy, starting from dU = TdS – PdV, we introduced G = U – TS + PV, resulting in a potential where T and P are the natural variables, dG = –SdT + VdP, and G is minimized when the natural variables are constrained. By introducing G’ = U – TS + PV – NHμH+ we arrive at a potential that is a natural function of pH. The variable NH is the number of hydrogens in the molecule. To obtain a transform that is also a natural function of pMg = –log[Mg2+], we use G’ = U – TS + PV – NHμH+ – NMgμMg2+. Standard-state transformed Gibbs energies of formation are developed for species, and they are used analogously to the untransformed Gibbs energies to calculate the Gibbs energy for reactions and the transformed equilibrium constant.
Also, to correct for solution nonidealities, the extended Debye-Hückel model is added, and a convention is to use Ba = 1.6 in the model. A further difference from previous models is that molar concentrations are used for the equilibrium constants, though it makes little difference numerically because solutions of biological molecules are typically dilute on a molar basis. The effect of nonidealities is typically calculated using the molal form of the Debye-Hückel model, using the overall solution molal ionic strength since the model does not differentiate between charged species.
Gibbs Energy Transformations for Species with a Single Form
For a species containing hydrogen or Mg,
Transformed Gibbs energy of formation at a specified pH and I. Workbook GprimeCalc.xlsx or MATLAB GprimeCalc.m are helpful.
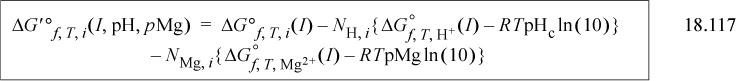
The Gibbs energy of formation appearing on the right side for j = i, H+, and Mg2+ is
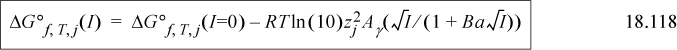
where Ba = 1.6 (kg/mol)½, pHc = –log[H+], pMg = –log[Mg2+], and I is measured in molality. By assuming that the heat of formation is independent of temperature in the small temperature range where biological reactions occur, the short-cut van’t Hoff equation can be applied before inserting the Gibbs energy of formation into
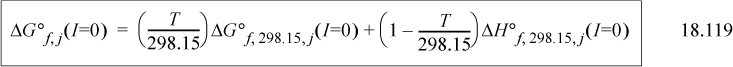
The equations are presented in the reverse order compared to how they are used. Standard state values are inserted into Eqn. 18.119 for j = i, H+, and Mg2+. The results are inserted into Eqn. 18.118 for each, and then each of those results is inserted into Eqn. 18.117. Conversion of the Gibbs energy of formation is easy using the Excel workbook GprimeCalc.xlsx or MATLAB m-file GprimeCalc.m. Note that the solution nonidealities are a minor correction compared to the transformations on H+ and Mg2+. The ’ notation is used quite widely for this transformed Gibbs energy at any specified pH, though in some literature the transformation is restricted to pH 7. The context of applications must be studied to discern if Mg2+ is included.
Enthalpy Transformations for Species with a Single Form
The enthalpy is obtained via the Gibbs-Helmholtz relation, where the heat of formation at I = 0, pH = 0, and pMg = 0 is independent of temperature as a first approximation. The Debye-Hückel temperature dependence introduces a correction. The heat of formation is
Transformed enthalpy of formation at a specified pH and I. Workbook GprimeCalc.xlsx or MATLAB GprimeCalc.m are helpful.
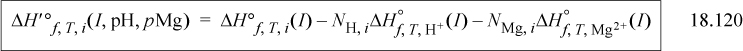
and for each enthalpy of formation on the right side, j = i, H+, and Mg2+:
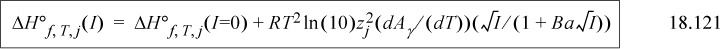
Gibbs Energy Transformations for Pseudoisomers
For families of receptors with different numbers of ligands, the transformed Gibbs energy of formation depends on the distribution of species, which changes with T, pHc, and pMg, but the dependence is easily represented by the binding polynomial. The Gibbs energy of formation for the apparent species takes a very simple modification relative to the Gibbs energy of formation of the completely bare receptor,
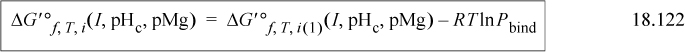
where G′o f, T, i(1)(I, pHc, pMg) on the right is for the completely bare receptor as determined by Eqns. 18.117–18.119. The binding polynomial can most easily be expressed in terms of the transformed Gibbs energies of formation of each pseudoisomer relative to the most bare receptor,
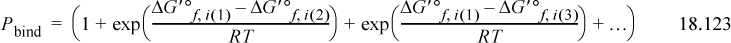
where all Gibbs energies are for aqueous solutions using Eqns. 18.117 – 18.119 at a specified pHc, pMg, and ionic strength, but the designations have been omitted for brevity. Alternative forms of Eqn. 18.123 are sometimes written, but the given form is recommended to avoid exponentials of very large or very small numbers because the differences in Gibbs energies of formation are much smaller than the values.30,31 Note that the exponential terms in Eqn. 18.123 are equivalent to the products of the equilibrium constants as shown in Eqn. 18.90.
The pHc, pMg, and nonideal solution effects are already incorporated into the reactions, and thus the binding polynomial in terms of the transformed equilibrium constants for phosphate would give
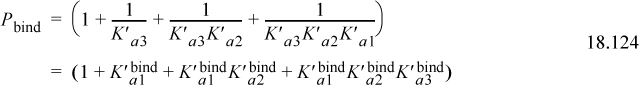
The fraction of receptor in each pseudoisomer form j in family i, can be calculated by two different methods. Pbind can be used directly, or we can use the transformed Gibbs energy of formation for the pseudoisomer with the transformed Gibbs energy of pseudoisomer form j,
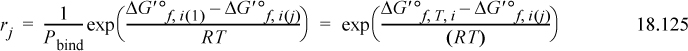
where all Gibbs energies are at the specified T, pH, and pMg. The argument of the first exp( ) is the same as used in 18.123, and the values of the first exp( ) are the same as the values for each term in Eqn. 18.124. The transformed enthalpy for the apparent species is most easily calculated by using the individual ri values where each pseudoisomer values is transformed by Eqn. 18.120,
This section has been intended as an introduction to biological thermodynamics. Readers interested in more depth will find more details in the work of Alberty31,32,33 or Goldberg.34 While the transformation of the standard state potentials shifts the standard state values of Gibbs energies, such that, for a reaction, ΔG′oT, i(I, pHc, pMg) ≠ ΔGoT, i(I, pHc, pMg), the actual driving force for a reaction at nonequilibrium conditions is the same,35 thus, ΔG′T, i(I, pHc, pMg) = ΔGT, i(I, pHc, pMg) as in Eqn 18.93 and in the analogous untransformed relation. Also, this means that K′c ≠ Kc, but the reaction is at equilibrium at the same true concentrations regardless of the transformation. This relation again emphasizes that the true driving force for the reaction is not represented by the standard state values.
Example 18.12. Gibbs energy of formation for ATP
The Gibbs energies of formation of ATP species are available in Appendix E. Using the available Gibbs energies, calculate the apparent Gibbs energy of formation for ATP at T = 298.15 K, pHc = 7, pMgc = 3, I= 0.25 mol/kg, the pK’, and the percentage of each species present.
Solution
The Gibbs energies for the molal standard state are ATP4– = –2768.1, HATP3– = –2811.48, H2ATP2– = –2838.18, MgATP2– = –3258.68, MgHATP– = –3287.5, and Mg2ATP = –3729.33 kJ/mol. The charges are –4, –3, –2, –2, –1, and 0, respectively. The number of H’s are 12, 13, 14, 12, 13, and 12, respectively. Inserting the values into GprimeCalc.xlsx, at the stated conditions, the transformed Gibbs energies of the species are ATP4– = –2291.9, HATP3– = –2288.8, H2ATP2– = –2270.7, MgATP2– = –2297.1, MgHATP– = –2282.7, and Mg2ATP = –2288.8 kJ/mol. The rest of the problem must be solved with hand calculations.
The third dissociation reaction is HATP3– 
ATP4–,
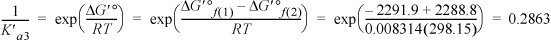
The product of the first and second is given by H2ATP2– ATP4–,
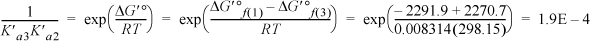
The remaining terms for HnATP(–4+n) in the binding polynomial are not important at pH = 7 because they will be even smaller than the last term calculated since the pH is far above the pKa (review Example 18.6 on page 718 for an analogy with phosphoric acid). For the species involving Mg, defining K′aMg for MgATP2– ATP4–,
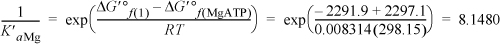
Defining K′aMgH for MgHATP– ATP4–,
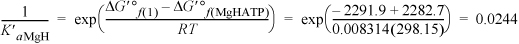
defining K′aMg2 for Mg2ATP ATP4–,
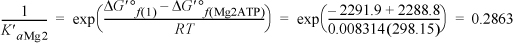
The binding polynomial is Pbind = 1 + 0.2863 + 2E–4 + 8.148 + 0.0244 + 0.2863 = 9.7452.
The fraction of each pseudoisomer is given by Eqn. 18.91:
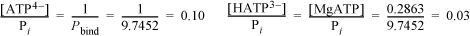
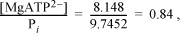
The other species make up the remainder and are insignificant at pH = 7.
The Gibbs energy of formation for the apparent species is
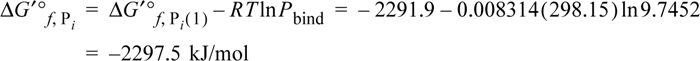
Note this is the value used in Example 18.10.
18.18. Coupled Multireaction and Phase Equilibria
Many texts are available to facilitate more advanced study. The following example uses thermochemical data from the OBIGT database documented in footnote 13 of this chapter. The example here is implement using the extended Debye-Hückel model and ignoring pressure corrections.
Chlorination of Water
Chlorination is one method of water treatment for drinking. When Cl2 dissolves in pure water, it undergoes reaction with water to simultaneously form the strong acid HCl and the weak acid hypochlorous acid (HClO). The reaction is sensitive to pH, and at low pH it is shifted toward molecular Cl2. At high pH, the reaction shifts to hypochlorous acid which is an oxidizer as well as a weak acid. Chlorine bleach is prepared by stabilizing the hypochlorous acid at high pH by reacting Cl2 with a solution of NaOH.
Consider the situation with pure water. There are three reactions to be taken into account:
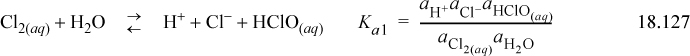
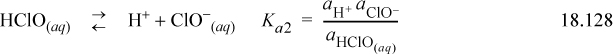
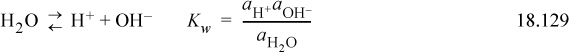
We can also write the liquid-vapor equilibria as “reactions,” noting the convention in the electrolyte literature is that the liquid phase is always the “product.” This is the convention used for Henry’s law constants (cf. Section 11.12) in Eqns. 18.130 and 18.131:
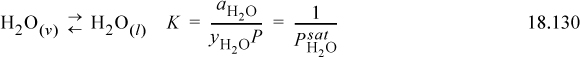
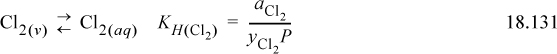
Example 18.13. Chlorine + water electrolyte solutions
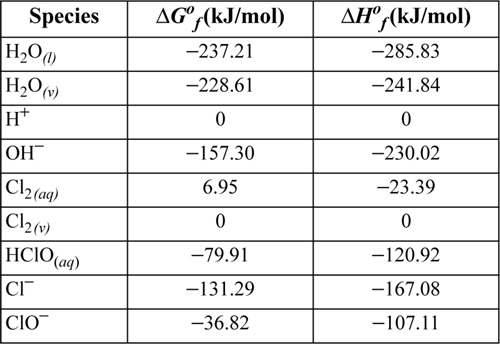
Determine the concentration and species present when chlorine is in equilibrium with water at 298.15 K and 0.8 atm. Develop an approximate solution and then use extended Debye-Hückel with Ba = 1 (kg/mol)1/2. Thermodynamic properties from the OBIGT documented in footnote 13 of this chapter are tabulated in Table 18.4.
Table 18.4. Thermochemical Data for the Species
Solution
We first work the problem assuming ideal solutions. This provides an approximate answer. Then we may use the activity coefficients to refine the answer. Using the Gibbs energies of formation, the equilibrium constants are: pKa1 = 3.339, pKa2 = 7.549, and KH(Cl2) = 0.0606, where KH is Henry’s constant for Cl2.
Since chlorine forms the strong acid HCl and the weak hypochlorous acid when dissolving in pure water, we expect pH < 7. Note that the weak hypochlorous acid should be almost totally protonated below pH = pK – 1 = 6.5. Since a strong acid HCl is being formed, this seems very likely. Let us proceed with that assumption. This enables us to disregard the dissociation of Eqn. 18.128 as a first approximation.
The three reaction equilibria are summarized in Eqns. 18.127–18.129. The charge balance is
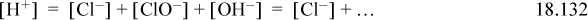
where [ClO–] is ignored because the dissociation of hypochlorous is small when the pH is small and [OH–] is ignored when pH is small. Thus, the equilibria of Eqn. 18.127 can be approximated as
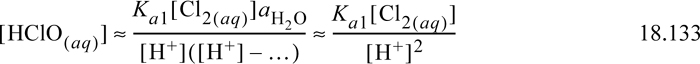
Approximate Solution:
The partial pressure for water can be estimated by first assuming that the water is almost pure. This approximation can be refined later if we find significant concentrations of chlorine species. We also use molar concentrations to approximate molalities. Using Raoult’s law for water, 
. From the steam tables, 
bar = 0.0313 atm, and yH2O = 0.0313/0.8 = 0.039. Then yCl2 P = 0.8 – 0.0313 = 0.7687 atm, yCl2 = 1 – 0.039 = 0.961. Using Henry’s law coefficient (KH) for Cl2 at 298.15 K, the concentration of Cl2(aq) is (independent of pH):
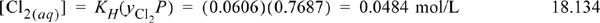
The concentration [HOCl(aq)] = 10–3.339(0.0484)/[H+]2 (Eqn. 18.133) at small values of pH is plotted in a Sillèn diagram. The weak acid dissociation of hypochlorous acid [OCl–] is to be calculated from Eqn. 18.31 using the concentration of [HOCl] as a function of pH. As expected, the dissociation is small at low pH.
The weak acid curve in Fig. 18.14 is much different from curves in previous examples because, in this case, the overall concentration of weak acid is changing rapidly with pH. Now consider the material balance associated with Eqns. 18.127 and 18.128. Since Eqn. 18.128 does not occur to a significant extent, to a good approximation by the stoichiometry of Eqn. 18.127 [H+] = [Cl–] = [HOCl]. This occurs at the intersection shown by the dotted lines. The approximate solution is pH = 1.55, [H+] = [Cl–] = [HOCl] = 10–1.55 = 0.0282 mol/L. Note on the diagram that [OCl–] = 10–7.5 = 3.2E-8. Now, we can use these as initial guesses in a more rigorous answer.
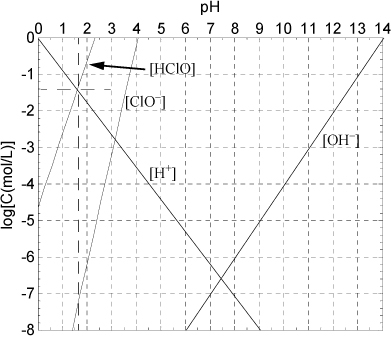
Figure 18.14. Determination of equilibria for the chlorine system.
Calculation with Activity Coefficients:
Thermodynamic properties for the components are tabulated below and in the spreadsheet: CL2H2O.xlsx. Note that the data tabulated below include values for Cl2 and H2O in both the vapor and aqueous phases. The Gibbs energies are used to calculate the VLE distribution coefficients as a “reaction.”
To solve the nine equations (five equilibria, three atom balances, and one charge balance) simultaneously, we must identify nine unknowns. The nine unknowns selected here are the species listed in Table 18.4: the liquid moles of H2O, Cl2, HClO, H+, Cl–, ClO–, and OH–, and the vapor moles of H2O(v) and Cl2(v). The basis is 1 liter of liquid water (niH2O = 55.51 moles) and niCl2 = 0.9 moles initially.
The detailed calculation are handled as a reactive flash. Three atom balances must be satisfied–H, O, Cl, along with the charge balance. The atom balances and charge balance are shown in Table 18.5 for the basis of 1 liter of liquid water and 0.9 moles of Cl2. The compositions for iteration are summarized in Table 18.6.
Table 18.5. Atom Balance and Electroneutrality Constraints
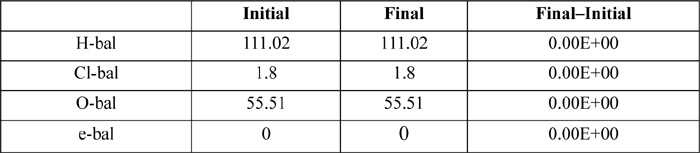
Table 18.6. Electrolyte Component Mole Numbers and Activities at the Converged Composition
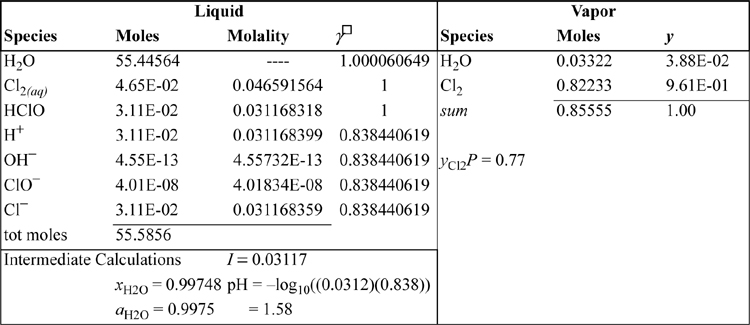
The results from the approximate ideal solution calculation above are used as initial guesses. Excel Solver is used to adjust the moles of each species (in the second and sixth columns of Table 18.6) until all equations are simultaneously satisfied.
Note from Table 18.6 that the γ□ for all the ionic species is the same. This occurs because the Debye-Hückel model is too simple to make distinctions as long as all species have the same valence. The activity coefficients for Cl2 and HClO are assumed to be unity.
The calculations summarized in Table 18.6 show that the chlorine solubility is enhanced beyond what might be predicted from the Henry’s law constant alone due to formation of HClO and Cl– in solution. The Cl in HClO and Cl– together is about two-thirds of the Cl atoms in Cl2(aq) at P = 0.8 atm. Open the spreadsheet Solver to see how the constraints were implemented. Compare with the approximate answer to see that the approximate answer is pretty close. For example, [HClO] = 0.0312 versus 0.0282.
Leave a Reply