Thermodynamic Network for Electrolyte Equilibria

Equilibrium Constants

Suppose an electrolyte has a chemical formula C₂A where C⁺ is a monovalent cation and A^2– is a bivalent anion. Succinic acid, H₂Succ, is an example of an electrolyte with this formula. An equilibrium network can be created as shown in Fig. 18.2. An electrolyte with an arbitrary C₂A composition is shown, with the expectation that readers can properly generalize the network for a specific electrolyte. If completely general notation was used, the figure notation would be unwieldy. While consideration of simultaneous equilibrium between solid, liquid, and vapor phases is rarely necessary, certain subsets of the general network are very common. For example, when an aqueous solution of succinic acid is saturated with solid H₂Succ, the aqueous solution contains H₂Succ, HSucc^2–, and H⁺ and the prevalence of a particular species depends on the pH, but the H₂Succ in the vapor is probably negligible.

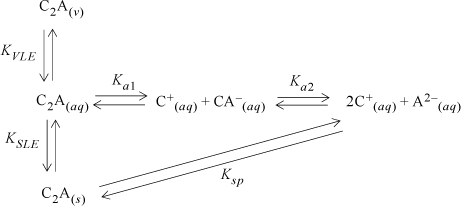
Figure 18.2. Reaction network for an example electrolyte where C is a monovalent cation and A is a divalent cation. The equilibrium constants are related as explained in the text.

Fig. 18.2 emphasizes that the undissociated electrolyte species is the key connection to vapor-liquid equilibria, and also can be used for solid-liquid equilibria. It is proven in Section 18.23 that the apparent chemical potential of C₂A in the liquid phase , is equal to the chemical potential of the dissolved undissociated species μ_i(aq):

This may seem odd in the case of a strong electrolyte where the amount of undissociated species is infinitesimal, but it is in fact rigorous. From an engineering perspective this apparent chemical potential is important because it is used to relate the apparent chemical potential to the component chemical potentials in the phases where the electrolyte is undissociated.

Note that the reaction for the solubility product constant

can be obtained by summing the reactions for melting along with the two dissociation reactions. Since the Gibbs energies are related to the logarithms of the equilibrium constants, we may write

Thus, the solubility of electrolytes is frequently written using the solubility product constant, K_sp instead of representing all the intermediate dissociation behavior. While this is rigorous thermodynamically using activities, an approximate solution is often used with concentrations rather than activities.

Whether a given electrolyte acts as a strong or weak electrolyte is sometimes unknown at the time a model is required for process design. In other cases, the electrolytes are assumed to act as strong electrolytes for convenience. A confusing aspect of the literature is that often the reader must infer whether a strong electrolyte model is applied depending on whether the dissociation constants are used. When a weak electrolyte is modeled using a strong electrolyte model, the adjustable activity model parameters can be forced to fit, but often the parameters are unusual. For example, when activity coefficients are determined for a weak electrolyte assuming that it is strong, the activity coefficients are very small. This is because the assumed “true” concentration of ions is much larger than the actual concentration, so the activity coefficients must be smaller than expected to match the experimental activities.