The van Laar Model

Johannes van Laar found that the parameters from the van der Waals equation of state were not accurate in predicting excess energy of mixing, and empirical fitting was required. He simplified the equation for the excess internal energy by arbitrarily defining a single symbol, “Q,” to represent the final term in the equation:

J. van Laar was a student of Johannes van der Waals and Jacobus Henricus van’t Hoff.

It would appear that this equation contains three parameters (V₁, V₂, and Q), but van Laar recognized that it could be rearranged such that only two adjustable parameters need to be determined.

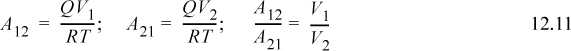
with the final result:⁵

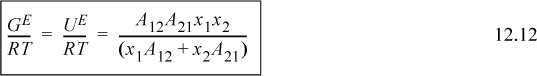
Differentiating Eqn. 12.12 gives expressions for the activity coefficients. To show this for γ₁,

Applying Eqn. 11.28 for n₁ and differentiating the ratio using the product rule on (n₂A₁₂A₂₁)(n₁)(1/(n₁A₁₂+n₂A₂₁)),

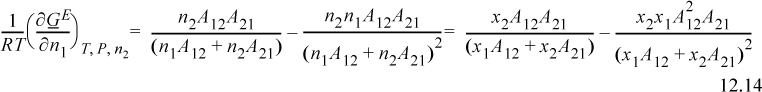
Obtaining a common denominator, rearranging, and applying symmetry for γ₂,

 Van Laar model.

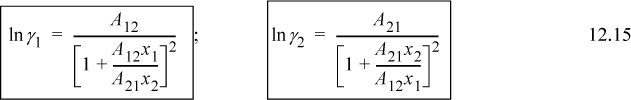
Note: The parameters A₁₂ and A₂₁ for the van Laar and Margules equations have different values for the same data. Do not interchange them.

When applied to binary systems, it is useful to note that these equations can be rearranged to obtain A₁₂ and A₂₁ from γ₁ and γ₂ given any one VLE point. This is the simple manner of estimating the parameters that we generally apply in this chapter. Similar to the two-parameter Margules, a single experimental point can be used as described in Section 11.6:

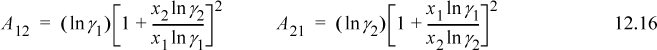
Care must be used before accepting the values of Eqns. 12.16 applied to a single experiment, because experimental errors can occasionally result in questionable parameter values. Eqn. 12.16 applied to the activity coefficients from Example 11.1 results in A₁₂ = 2.38, A₂₁ = 1.15, and G^E is plotted in Fig. 11.3. Methods of fitting the parameters in optimal fashion for many data are covered in Section 11.9.

---

Example 12.1. Infinite dilution activity coefficients from the van Laar theory

n-Propyl alcohol (1) forms an azeotrope with toluene (2) at x₁ = 0.6, 92.6°C, and 760 mmHg. Use the van Laar model to estimate the infinite dilution activity coefficients of these two species at this temperature.

Solution

The vapor pressures using parameters from Antoine.xlsx are , .

Applying the azeotropic data as explained in Section 11.7 gives:  = 1.191; . Eqn. 12.16 gives: A₁₂ = 1.643; A₂₁ = 1.193.

Taking the limits of Eqn. 12.15 as the respective components approach zero composition results in  and ; Similarly .

---

Linear Fitting of the van Laar Model

Like the Margules models, the van Laar model can be linearized. Eqn. 12.12 can be rearranged:

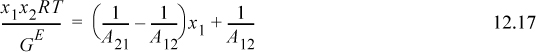
Therefore, if numerical values for the left-hand side are determined using G^E from experimental data as illustrated in Example 11.1 on page 414 and plotted versus x₁, the slope yields (1/A₂₁ – 1/A₁₂), and the intercept yields 1/A₁₂. The value of 1/A₂₁ can also be determined by the value at x₁ = 1. Sometimes plots of the data are non-linear when fitting is attempted. This does not necessarily imply that the data are in error. It implies that an alternative model may fit the data better. By plotting the data in both the Margules and van Laar linearized forms, the better model can be identified as the one that is most linear. Fitting the data for 2-propanol + water presented in Example 11.8 (ignoring the first mixture point), results in an intercept = 1/A₁₂ = 0.4993, slope = 0.3486, resulting in A₁₂ = 2.00, A₂₁ = 1.18.