Empirical models like the Redlich-Kister expansion provide a significant improvement over the ideal solution approximation, but they lack the kind of connection with the molecular perspective that we have developed in Chapters 1 and 7. The empirical models of Chapter 11 are useful for determining the activity coefficients from a given expression for GE, but they suggest little about the form that GE should assume. As we develop models that incorporate physical insight more closely, we also obtain greater predictive power.
Section 12.1 introduces concepts common to many models based on the van der Waals approach including random mixing rules and the use of the “regular solution” assumption. Section 12.2 introduces the van Laar equation which has a meaningful functional form, but, like the Redlich-Kister and Margules equations, is fitted to experimental data. Section 12.3 introduces the Scatchard-Hildebrand theory, which represents historically the first widely-accepted predictive model, primarily useful for mixtures of nonpolar molecules. Though the original theory has limited direct use today, it is the basis of several other models, and solubility parameters developed therein are currently widely-used to characterize solvents. Section 12.4 develops the Flory equation and the Flory-Huggins model that combines the Flory representation of entropy of mixing with the Scatchard-Hildebrand theory for energy of mixing. The Flory-Huggins approach is widely used in polymer thermodynamics. Section 12.5 extends the Scatchard-Hildebrand theory by including acidity and basicity corrections in a manner that is very successful in estimating infinite dilution activity coefficients. That section also develops the SSCED and MAB models, which are pedagogical simplifications that apply the concepts with approximate methods. The final sections document the relation of the theories to the original van der Waals equation, and extend the models to multicomponent systems.
Chapter Objectives: You Should Be Able to…
1. Compute VLE phase diagrams using modified Raoult’s law with the van Laar, Scatchard-Hildebrand, SSCED, MOSCED, or Flory-Huggins models.
2. Compute the relative volatility of key components in a multicomponent mixture.
3. Explain the relationship between molecular properties like energy density, acidity, and basicity and macroscopic behavior like activity coefficients and azeotropes, enabling predictions and formulation design.
12.1. The van der Waals Perspective for Mixtures
We have seen that the van der Waals EOS in Chapter 7 provides a simple basis for understanding the interplay between entropy, energy, repulsion, and attraction of pure fluids. Even the embellishments of the Peng-Robinson equation add little to the qualitative physical picture envisioned by van der Waals. Therefore, the van der Waals model provides a reasonable starting point for conceiving the physics of mixtures. The key quantities to be considered are van der Waals’ a and b. If only we knew how to compute a = a(x) and b = b(x), then we could solve for Z for a mixture. Through Z, we can integrate our density-dependent formulas to obtain G, then differentiate with respect to composition to obtain partial molar Gibbs energies, chemical potentials, and component fugacities. This is the general strategy. The formulas for a = a(x) and b = b(x) are called mixing rules.
A Simple Model for Mixing Rules
Recognizing the significance of the Gibbs excess function, it should not be surprising that many researchers have studied its behavior and developed equations that can represent its various shapes. In essence, these efforts attempt to apply the same reasoning for mixtures that was so successful for pure fluids in the form of the van der Waals equation. The resultant expressions contain parameters that are intended to characterize the molecular interactions within the context of the theory. The utility of the theory is judged by how precisely the experimental data are correlated and by how accurately predictions can be made. Given that molecules in solution must actually interact according to some single set of laws of nature, one might wonder why there are so many different theories. The challenge with mixtures is that there are many different kinds of interactions occurring simultaneously, for example, disperse attractions, hydrogen bonding, size asymmetries, branching, rings, and various rotations and aspect ratios. As a result, many specific terms must be invoked to describe these many specific interactions. Because incorporation of all these effects makes the resultant model unwieldy, many researchers have made different approximations in their models. Each model has its proponents. It is difficult even to describe the various models without expressing personal prejudices. For practical applications, the perspective we adopt is that these equations usually fit the data, and that extrapolations beyond the experimental data must be performed at some risk.
The models considered in the remainder of this chapter are based on extension of the van der Waals equation of state (Eqn. 7.12) to the energy departure for mixtures. When we extend equations of state to mixtures, the basic form of the equation of state does not change. The fluid properties of the mixture are written in terms of the same equation of state parameters as for the pure fluids; however, equation of state parameters like a and b are functions of composition. The equations we use to incorporate compositional dependence into the mixture constants are termed mixing rules.
The composition dependence is introduced into an equation of state by mixing rules for the parameters. The basic equation form does not change.
The parameter b represents the finite size of the molecules. For many mixtures of roughly equal-sized molecules, the dense volumes mix ideally. Therefore, it is reasonable to assume2
As for a, we must carefully consider how this term relates to the internal energy of mixing, because the Gibbs energy of mixing is closely related. The departure function can be quickly found using Eqn. 7.12 with the departure formula Eqn. 8.22, resulting in
The parameter a should represent the average attraction resulting from the many varied molecular interactions in the mixture.
In a binary mixture there are three types of interactions for molecules (1) and (2). First, a molecule can interact with itself (1+1 or 2+2 interactions), or it can interact with a molecule of the other type (a 1+2 interaction). Assuming a random fluid,3 the probability of finding a (1) molecule is the fraction of (1) atoms, x1. The probability of a 1+1 interaction is a conditional probability. A conditional probability is the probability of finding a second interacting molecule of a certain type given the first is a certain type. For independent events, a conditional probability is calculated by the product of the individual probabilities. Therefore, the probability of a 1+1 interaction is 
. By similar arguments, the probability of a 2+2 interaction is 
. The probability of a 1+2 interaction is x1x2 and the probability of a 2+1 interaction is also x1x2.4 If the attractive interactions are characterized by a11, a22, and a12, the mixing rule for a is given by:
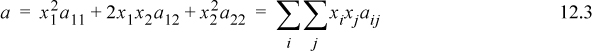
where the pure component a parameters are indicated by identical subscripts on a. In other words, a11 represents the contribution of 1+1 interactions, a22 represents 2+2 interactions, a12 represents the contribution of 1+2 interactions, and the mixing rule provides the mathematical method to sum up the contributions of the interactions. a12 is called the cross coefficient, indicating that it represents two-body interactions of unlike molecules. In the above sum, it is understood that a12 is equivalent to a21. Note that a12 is not the a for the mixture. This type of mixing rule is called a quadratic mixing rule, because all cross-products of the compositions are included. It represents a fairly obvious approximation to the way mixing should be represented.
The quantity a12 plays a major role in the solution behavior. Predicting solution behavior is largely the same task as predicting a12. This prediction takes the form of
where k12 is an adjustable parameter called the binary interaction parameter. The default is k12 = 0, giving a preliminary estimate of a12. Going beyond this estimate requires contemplating whether we expect positive or negative deviations from Raoult’s law. Eqns. 12.3 and 12.2 show that larger values of a12 result in more negative (exothermic) energies of mixing. More negative values of k12 lead to more negative energies of mixing, which is favorable to mixing.
We can relate a12 to the molecular properties by considering the square-well model. Fig. 1.2 shows the square-well model for a binary mixture. We are now in a better position to interpret its significance. When k12 is positive (case (c)), the depth of the attraction is shallower. The most positive value would be k12 = 1, in which case there would be no attraction at all. This is an easy way to remember that positive values of k12 lead to repulsion. When k12 is negative (case (b)), the attraction can be very deep. In fact, k12 < –1 is a possibility for very strong acid-base interactions. Recalling our discussion of the MAB model, we should begin to understand how to predict k12. We further develop this understanding through the remaining discussion in this chapter.
Activity Models from the van der Waals Perspective
Several models derive from the van der Waals equation of state with the assumption of a constant packing fraction (bρ). They are distinguished by different approximations of the terms in the resultant equations. For example, the entropic contributions to GE are neglected by “regular” solution models (van Laar, Scatchard-Hildebrand, SSCED). The van Laar model is distinguished by treating the ratio of V2/V1 as an adjustable parameter, whereas Scatchard-Hildebrand and SSCED estimate that ratio from the liquid molar volume. SSCED differs from Scatchard-Hildebrand by accounting for the effects of hydrogen bonding (like the MAB model) as well as the influences of attractive dispersion forces (aρ).
Many of these distinctions may seem superficial, but they are part of the historical development that forms the lexicon of activity models. Furthermore, they provide a convenient shorthand for referencing the various contributions to overall solution behavior. It is important to remember, however, that the assumed activity model in no way alters the procedures for computing VLE developed in Chapters 10 and 11. You should be able to adapt any solution model to solving VLE problems by simply substituting the appropriate expression for γ.
“Regular” Solutions
The Gibbs energy, GE = UE + PVE – TSE, is composed of three contributions. For liquids, the PV term is small to begin with, and PVE is even smaller, so it makes sense to ignore the excess volume contribution and assume that the solution volume follows ideal mixing rules. Recalling how entropy is related to volume suggests the hypothesis that entropy might mix ideally also. These simple suppositions lead to the theories of van Laar or Scatchard and Hildebrand. We refer to “regular solution theories” when applying the assumptions of VE = SE = 0, leading to GE ≈ UE.
The energetics of a of the mixture are given by Eqn. 12.3 and 12.4. For the volume, assuming zero excess volume, 
according to regular-solution theory. Combining into Eqn. 12.2,
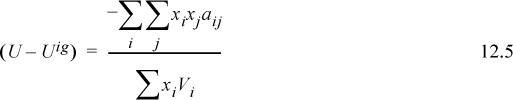
For the pure fluid, taking the limit as xi → 1,
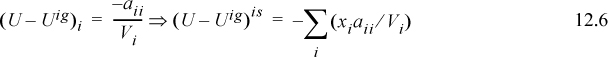
For a binary mixture, subtracting the ideal solution result, UE = (U – Uig) – (U – Uig)is to get the excess energy gives,
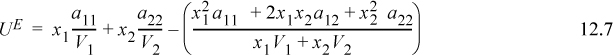
Collecting terms over a common denominator,
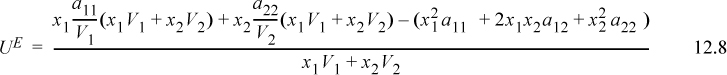
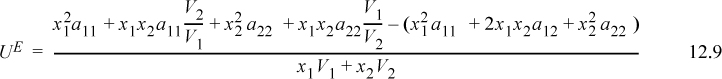
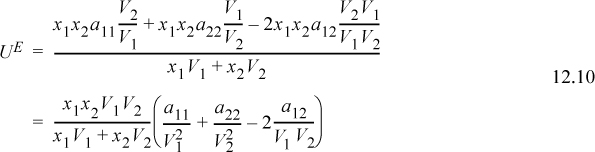
Leave a Reply