Our common experience tells us that oil and water do not mix completely, even though both are liquids. If we consider equilibria between the two liquid phases, we can label one phase α and the other β. For such a system we can quickly show that the equilibrium compositions are given by
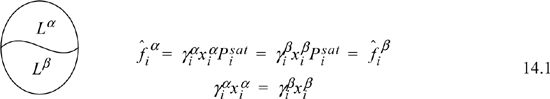
where superscripts identify the liquid phase. The coexisting compositions are known as mutual solubilities. Note that we have assumed an activity coefficient approach here even though we could formulate an entirely analogous treatment by an equation of state approach. There is also the possibility that three phases can coexist, two liquids and a vapor, which is illustrated below and is known as vapor-liquid-liquid equilibria, or VLLE. In this case we have an additional fugacity relation for the gas phase, where we assume in the figure that the ideal gas law is valid for the vapor phase. An example of how such a system could be solved is given below. The phase equilibria can be solved by starting with whichever two phases we know the most about, and filling in the details for the third phase.
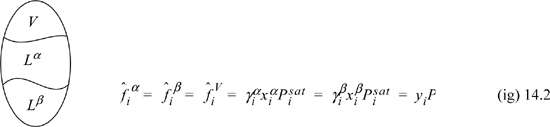
Example 14.1. Simple vapor-liquid-liquid equilibrium (VLLE) calculations
At 25°C, a binary system containing components 1 and 2 is in a state of three-phase LLVE. Analysis of the two equilibrium liquid phases (α and β) yields the following compositions:

Vapor pressures for the two pure components at 25°C are ![]() and
and ![]() .
.
Making reasonable assumptions, determine good estimates for the following.
a. The activity coefficients γ1 and γ2 (use Lewis-Randall standard states).
b. The equilibrium pressure.
c. The equilibrium vapor composition.
Solution
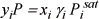
Assume ![]() because these are practically pure in the specified phases.
because these are practically pure in the specified phases.
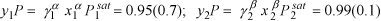
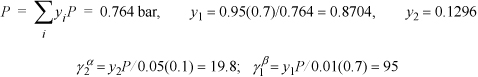
We also can determine activity coefficients from a theory to determine infinitely dilute concentrations. When a phase is nearly pure, the activity coefficient is nearly one at the same time xi is nearly one.
Example 14.2. LLE predictions using Flory-Huggins theory: Polymer mixing
One of the major problems with recycling polymeric products is that different polymers do not form miscible solutions with each other, but form highly nonideal solutions. To illustrate, suppose 1 g each of two different polymers (polymer A and polymer B) is heated to 127°C and mixed as a liquid. Estimate the mutual solubilities of A and B using the Flory-Huggins equation. Predict the energy of mixing using the Scatchard-Hildebrand theory. Polymer data:

Solution
This is the same mixture that we considered as an equal-weight-fraction mixture in Example 12.5. Based on that calculation, we know that the solution is highly nonideal. We must now iterate on the guessed solubilities until the implied activity coefficients are consistent. Let’s start by guessing that the two polymer phases are virtually pure and infinitely dilute in the other component.
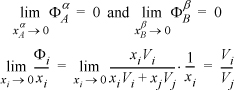
Using Eqns. 11.46 and 11.47,
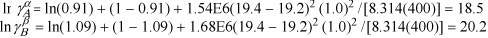
Since ![]() , then
, then ![]() and
and ![]() .
.
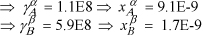
Good guess. The polymers are totally immiscible. No further iterations are needed.
Leave a Reply