The Molecular Basis of Solution Models

As discussed during the development of quadratic mixing rules, there comes a point at which the assumption of random mixing cannot completely explain the nonidealities of the solution. Local compositions are examples of nonrandomness. The popularity of local composition models like Wilson’s equation or UNIFAC means that we need to develop some appreciation of the strength of the underlying theory and its limitations. Similar to the situation for the random mixing models, there are limitations to the local composition models. At this time, however, we are not exactly sure what all the limitations are. This is still a question for active research. Nevertheless, we can provide an understanding of the assumptions in these models, because the assumptions are the sources of errors that impose limitations.

Extending the Energy Equation to Mixtures

We begin the discussion with the energy equation, not the pressure equation as we did for pure fluids. This is because we are presently concerned with the Gibbs energy of mixing and its excess change relative to ideal solution behavior. It turns out that the excess Gibbs energy is dominated by the excess internal energy in most cases. In other words, the entropy of mixing is given with reasonable accuracy by the mixing rule on “b” given in Eqn. 12.1. Therefore, we focus our attention on extending the energy equation to mixtures. This requires revisiting our development of the energy equation for pure fluids and applying the same principles to extend it to mixtures. With two small modifications, the energy equation we developed for pure fluids becomes:

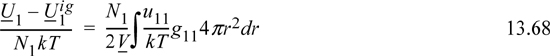
The small modifications are: (1) We have put the equation on an atomic basis instead of a molar basis by noting n_iN_A = N_i and Nk = nR; (2) We recognize that these are the contributions to the energy departure that arise from atoms of type “1.” For the pure fluid, it so happens that we only have atoms of type “1.”

In developing the energy equation for pure fluids, we recognized that the average internal energy departure per atom [i.e., (U₁ – U₁^ig)/N₁] was equal to the energy per pair per unit volume times the local density in that volume integrated over the total volume. To make the extension to a mixture, we must simply recognize that there are now atoms of “type 2” around those atoms of “type 1.” To illustrate, consider a parking lot full of blue cars and green cars. If one parking lot had only green cars, then the average energy per green car would involve the average number of green cars at each distance around one green car times the energy associated with green cars being that distance from each other. If you pack them too close, you will have to work hard to pack them, and so forth. Now consider the next parking lot, where blue cars are mixed with green cars. The average energy per green car will now involve contributions from green-green interactions and blue-green interactions. In equation form, this becomes

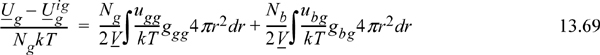
We can check this equation by noting that it approaches the pure green car equation when all the blue cars leave the parking lot (i.e., as N_b → 0). We may next write the average energy per blue car by symmetry and the total energy by addition.

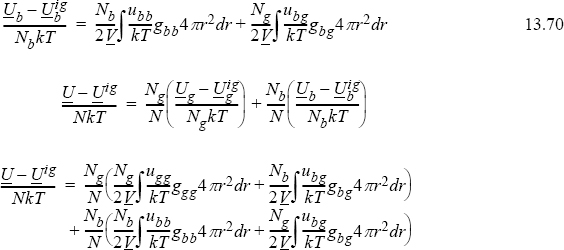
Finally, making the substitutions in terms of the mole fractions, recognizing that u_bg=u_gb and g_bg=g_gb, and converting back to a molar basis, we see that for multicomponent mixtures,

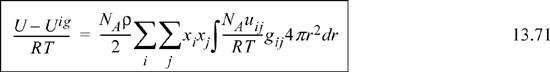
 The energy equation for mixtures.

Comparing to the van der Waals equation for pure fluids,

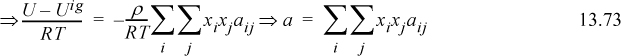
where  and it is understood that a_ij = a_ji.

In this form we can recognize that the radial distribution functions may be dependent on composition as well as temperature and density. Therefore, assuming the quadratic mixing rule simply neglects the composition dependence of the a parameter, as well as the temperature and density dependence. We found in Unit II that the assumptions about temperature and density in the van der Waals equation were flawed and that is what motivated the Peng-Robinson equation. Similarly, neglecting the composition dependence of the radial distribution functions leads to some limitations that give rise to local composition theory.

Local Compositions in Terms of Radial Distribution Functions

Recalling the energy equation for mixtures, Eqn. 13.71 multiplied by RT,

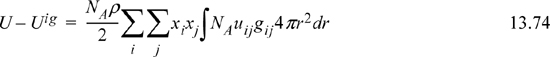
We may now define the local compositions in terms of the radial distribution functions.

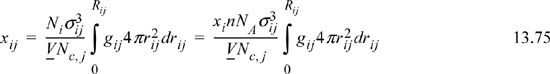
where r_ij = r / σ_ij

          R_ij = “neighborhood”

          N_c,i = total # of atoms around sites of type “i,” that is, the coordination number.

Rearrangement gives the molecular definition of the local composition parameter Ω_ij,

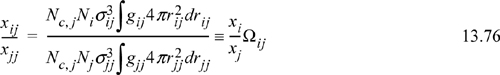
and we note the similarity between the integral in the energy equation and the integral in the definition of local composition.

For a square-well fluid, ε_ij = constant, so we can factor it out of the integral,

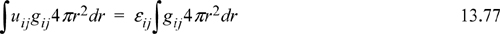
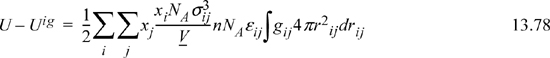
Substituting N_c,j, and x_ij into the energy equation for mixtures (multiply Eqn. 13.75 by N_c,j and substitute into Eqn. 13.78),

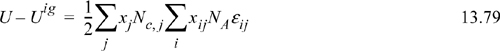
This is the equation previously applied as the starting point for development of the Gibbs excess energy model from a local composition perspective. The rest of the derivation proceeds as before.

Assumptions in Local Composition Models

In the previous section, we discussed some of the currently popular expressions for activity coefficients. We listed the assumptions involved in developing the expressions but we did not take time to discuss those assumptions. Instead, we directly applied the expressions as a practical necessity and moved on. In this section, we recall those assumptions and attempt to put them in perspective. After developing this perspective, we conclude with a word of caution; the reliability of the predictions depends largely on the accuracy of the assumptions.

The local composition theory, upon which UNIQUAC and others are based, has the general intent of correcting regular solution theory for asymmetries in solution behavior due to fluid structure near a central species. Relaxing the assumption that S^E = 0 also leads to the necessity of considering the entropy of mixing, and differences between the UNIQUAC model and Wilson’s model are primarily due to differences in treatment of S^E. In review, four assumptions are shared by the local composition theories when considered with respect to spheres:

1. The average energy of an i-j interaction is independent of temperature, density, and other species present.

2. (A – A^is) = (G – G^is).

3. The “coordination number” of a specie in a mixture is the same as that of the pure species.

4. The temperature-dependent part of the energy of mixing is given by Ω_ij = (σ_ij/σ_ij)³ exp[z(ε_ij – ε_jj)/2kT] where z is a “coordination number.”

Wilson’s equation makes the following assumptions:

5w. N_c,j = z = 2 for all j at all densities.

6w. .

7w. (σ_ij/σ_jj)³ = V_i/V_j for all i, j, and , Λ_ji = Ω_ij.²⁰

UNIFAC(QUAC) makes the following assumptions:

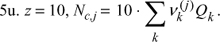
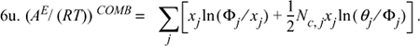
7u. (σ_ij/σ_jj)³ = N_c,i/N_c,j = q_i/q_j for all i, j, .

Assumption 1 involves factoring some average energy out of the energy integral such that the local composition integral is obtained. As noted, this assumption would be correct for a square-well potential, so we can probably trust that it would be reasonable for other similar potentials like the Lennard-Jones. The doubt which arises, however, involves the application of this approximation to highly nonideal mixtures. The square-well and Lennard-Jones potentials rarely give rise to highly nonideal mixtures when realistic values for their parameters are chosen. There is very little evidence to judge whether the ε_ij factored out in this way is really independent of temperature and density for nonideal mixtures. In fact, in Chapter 1, we showed that dipole interactions are temperature dependent.

Assumption 2 has to do with neglecting ln(Z/Z^is). For liquids, this may seem dangerous until one realizes that it amounts to neglecting ln(1 + ρ^E/ρ) ≈ ρ^E/ρ. Relative to the density of a liquid, the excess density is generally small (but easy to measure with a high degree of accuracy) and this assumption is acceptable.

Assumption 3 has to do with convenience. If the coordination number of each species was assumed to change with mixing, the theory could become very complicated. That is not a very good physical reason, of course. Physically speaking, this assumption could become quite poor if the sizes of the molecules (or segments in the case of UNIFAC) were very different.

Assumption 4 is the primary assumption behind all of the current local composition approaches, but it is not required by the concept of local compositions. It is simply computationally expedient in the equations that develop. The crucial aspect of the assumption is the simple form of the temperature dependence of Ω_ij. The main motivation for this assumption appears to be obtaining an expression which can be integrated analytically. But how accurate is this assumption on a physical basis? Moreover, how can we determine the physical behavior for the behavior of Ω_ij in an unequivocal manner? Merely fitting experimental data for the Gibbs excess function is equivocal because some set of adjustable parameters will provide a good fit even if the model has no physical basis. An alternative available to us that was not available to van der Waals is to apply computer simulation of square-well mixtures over a specific range of densities and temperatures and test the validity of Wilson’s approximation directly through the simulated local compositions. This approach was undertaken by Sandler and Lee.²¹

Sandler and Lee have developed a correlation for what amounts to Ω_ij of a square-well potential.

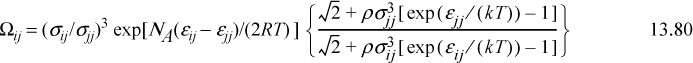
This expression reproduces the local compositions of a substantial set of molecular simulation data which Sandler and coworkers have generated. We can therefore use this expression along with the molecular simulation data as a guide to the accuracy of Wilson’s assumption.

The most important consideration is the temperature dependence of this parameter because it is the integration with respect to temperature that allows us to get from energy to free energy. As for density, it could be argued that the density of all liquids is roughly the same, so it is not unreasonable to pick a specific density and just study the temperature effects. Suppose

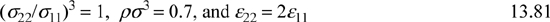
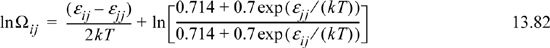
If the natural logarithm term on the right-hand side in the above equation is small or gives rise to a contribution which is linear in 1/kT, then Wilson’s assumption is basically correct and his definition of ε_ij would just be a little different from Eqn. 13.18. If ln Ω_ij versus 1/kT is not linear, however, then Wilson’s assumption is very questionable. Fig. 13.4 shows ln Ω_ij is fairly linear over certain ranges of temperature. This suggests that the primary assumption of Wilson and UNIFAC(QUAC) is not unreasonable. Does this mean that the problem of nonideal solutions is solved? Maybe, but maybe not. Unfortunately, we must look closely at the range of temperatures that are applicable. This range is limited by the tendency for the mixture to phase-separate. That is, dropping the temperature at constant overall density eventually places the conditions inside the binodal curve. For the composition and density listed above, the binodal occurs when N_A(ε₁₂ – ε₁₂)/RT < –0.4. This corresponds to a maximum value of A₁₂ in Wilson’s equation on the order of ~300 cal/mol at temperatures near 400 K. To use larger values for A₁₂ would be unsupported, but larger values are often used, as illustrated in Example 13.3.

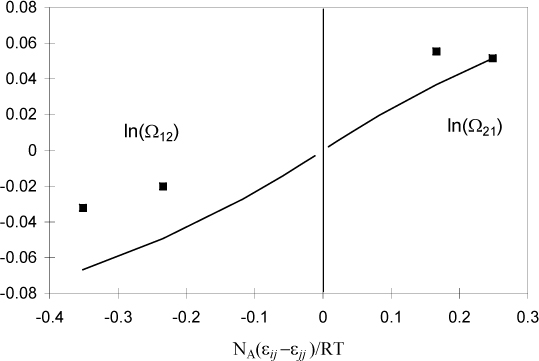
Figure 13.4. Temperature-dependence of local composition parameters. Points are molecular simulation data and the curve is the correlation of Sandler and Lee.²¹ The approximate linearity of the plot lends support to the assumption applied in integrating the internal energy to obtain the free energy.

Another indication of the potential for error with the local composition approach is given by experimental data for excess enthalpies of mixing. Relations from classical thermodynamics make it possible to estimate the enthalpy of mixing by taking the derivative of the Gibbs energy of mixing with respect to temperature. Larsen et al., have developed a modified form of UNIFAC to address this problem.²² Not surprisingly, the modification involves the introduction of a substantial number of additional adjustable parameters. Even though the modified form does improve the accuracy of all the thermodynamic properties for a large number of systems there are many systems for which the predicted heats of mixing are in error by 100%–700%. More importantly, there is no way of knowing in advance when the predictions will be in error or when they will be accurate.

So why do these approximations fit the activity coefficient data? Because they have enough adjustable parameters to fit the data. Even the Margules one-parameter equation is good enough for that in many cases, but we suffer few delusions about its physical accuracy. In conclusion, we must say that local composition theory has much to recommend it. It does fit a great wealth of experimental data and there is some justification for its form via the theoretical physics which can be applied. But it is often extrapolated too far and that can lead to miscalculations by unwary users. In the end, we must never underestimate the value of experimental data for nonideal mixtures and apply the currently available theory with a careful and mildly critical view.

Assumptions 5 through 7 have to do with the entropy of mixing. The inclusion of the Staverman-type modifications to address the differences between surface fraction and volume fraction are generally recognized to be reasonable based on polymer lattice computer simulations. This modification and the estimate of molecular volumes by group contributions instead of liquid molar volumes comprise the primary differences between the Wilson and UNIQUAC models.

The UNIFAC theory is distinguished from UNIQUAC in that the solution is assumed to be a mixture of functional groups, not molecules. The UNIQUAC theory is then applied to each type of group interaction. The values for the group interactions are then regressed from a data base that includes phase equilibrium data for many, many systems. In one sense, the UNIFAC method is more like a massive regression than a truly predictive method. Thus, it lies somewhere between the purely correlative method of fitting van Laar constants and the purely predictive method of the Scatchard-Hildebrand theory (or any equation of state with k_ij = 0). Like any regressed equation, it can be unreliable if extrapolated far beyond the originally applied data. If you are ever in the position of designing truly novel chemical systems, you should be especially sensitive to the need for specific experimental data.