The Departure Function Pathway

Suppose we desire to calculate the change in U in a process which changes state from (V_L, T_L) to (V_H, T_H). Now, it may seem unusual to pose the problem in terms of T and V, since we stated above that our objective was to use T and P. The choice of T and V as variables is because we must work often with equations of state that are functions of volume. The volume corresponding to any pressure is rapidly found by the methods of Chapter 7. We have two obvious pathways for calculating a change in U using {V, T} as state variables as shown in Fig. 8.1. Path A consists of an isochoric step followed by an isothermal step. Path B consists of an isothermal step followed by an isochoric step. Naturally, since U is a state function, ΔU for the process is the same by either path. Recalling the relation for dU(T,V), ΔU may be calculated by either.

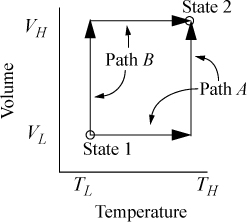
Figure 8.1. Comparison of two alternate paths for calculation of a change of state.

Path A:

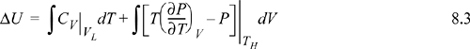
or Path B:

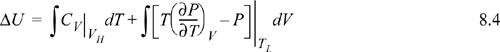
We have previously shown, in Example 7.6 on page 269, that C_V depends on volume for a real fluid. Therefore, even though we could insert the equation of state for the integrand of the second integral, we must also estimate C_V by the equation of state for at least one of the volumes, using the results of Example 7.6. Not only is this tedious, but estimates of C_V by equations of state tend to be less reliable than estimates of other properties.

To avoid this calculation, we devise an equivalent pathway of three stages. First, imagine if we had a magic wand to turn our fluid into an ideal gas. Second, the ideal gas state change calculations would be pretty easy. Third, at the final state we could turn our fluid back into a real fluid. Departure functions represent the effect of the magic wand to exchange the real fluid with an ideal gas. Being careful with signs of the terms, we may combine the calculations for the desired result:

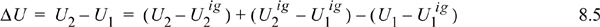
The calculation can be generalized to any fundamental property from the set {U,H,A,G,S}, using the variable M to denote the property

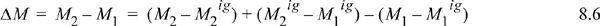
 Departure functions permit us to use the ideal gas calculations that are easy, and incorporate a departure property value for the initial and final states.

The steps can be seen graphically in Fig. 8.2. Note the dashed lines in the figure represent the calculations from our “magic wand” effect of turning on/off the nonidealities.

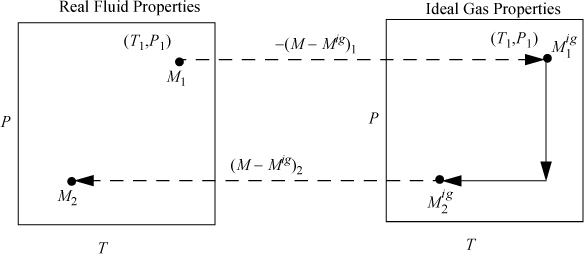
Figure 8.2. Illustration of calculation of state changes for a generic property M using departure functions where M is U, H, S, G, or A.

Note how all the ideal gas terms in Eqns. 8.5 and 8.6 cancel to yield the desired property difference. A common mistake is to get the sign wrong on one of the terms in these equations. Make sure that you have the terms in the right order by checking for cancellation of the ideal gas terms. The advantage of this pathway is that all temperature calculations are done in the ideal gas state where:

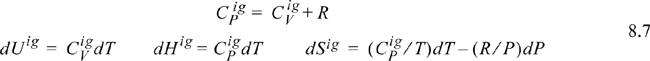
and the ideal gas heat capacities are pressure- (and volume-) independent (see Example 6.9 on page 242).

To derive the formulas to be used in calculating the values of enthalpy, internal energy, and entropy for real fluids, we must apply our fundamental property relations once and our Maxwell’s relations once.