The Clausius-Clapeyron Equation

We can apply these concepts of equilibrium to obtain a remarkably simple equation for the vapor-pressure dependence on temperature at low pressures. As a “point of view of greatest simplicity,” the Clausius-Clapeyron equation is an extremely important example. Suppose we would like to find the slope of the vapor pressure curve, dP^sat/dT. Since we are talking about vapor pressure, we are constrained by the requirement that the Gibbs energies of the two phases remain equal as the temperature is changed. If the Gibbs energy in the vapor phase changes, the Gibbs energy in the liquid phase must change by the same amount. Thus,

dG^L = dG^V

Rewriting the fundamental property relation ⇒ dG = V^V dP^sat – S^V dT = V^L dP^sat – S^L dT and rearranging,

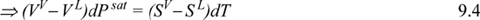
Entropy is a difficult property to measure. Let us use a fundamental property to substitute for entropy. By definition of G: G^V = H^V – TS^V = H^L – TS^L = G^L

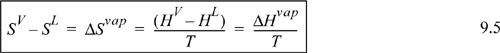
Substituting Eqn. 9.5 in for S^V – S^L in Eqn. 9.4, we have the Clapeyron equation which is valid for pure fluids along the saturation line:

 Clapeyron equation.

Note: This general form of Clapeyron equation can be applied to any kind of phase equilibrium including solid-vapor and solid-liquid equilibria by substituting the alternative sublimation or fusion properties into Eqn. 9.6; we derived the current equation based on vapor-liquid equilibria.

Several simplifications can be made in the application to vapor pressure (i.e., vapor-liquid equilibium). To write the equation in terms of Z^V and Z^L, we multiply both sides by T² and divide both sides by P^sat:

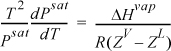
We then use calculus to change the way we write the Clapeyron equation:

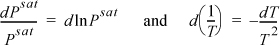
Combining the results, we have an alternative form of the Clapeyron equation:

 Clapeyron equation.

For a gas far from the critical point at “low” reduced temperatures, Z^V – Z^L ≈ Z^V. In addition, for vapor pressures near 1 bar, where ideal gas behavior is approximated, Z^V ≈ 1, resulting in the Clausius-Clapeyron equation:

 Clausius-Clapeyron equation.

---

Example 9.1. Clausius-Clapeyron equation near or below the boiling point

Derive an expression based on the Clausius-Clapeyron equation to predict vapor-pressure dependence on temperature.

Solution

If we assume that ΔH^vap is fairly constant in some range near the boiling point, integration of each side of the Clausius-Clapeyron equation can be performed from the boiling point to another state on the saturation curve, which yields

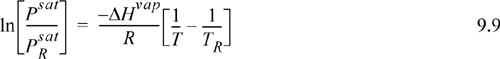
where  is 0.1013 MPa and T_R is the normal boiling temperature. This result may be used in a couple of different ways: (1) We may look up ΔH^vap so that we can calculate P^sat at a new temperature T; or (2) we may use two vapor pressure points to calculate ΔH^vap and subsequently apply method (1) to determine other P^sat values.

One vapor pressure point is commonly available through the acentric factor, which is the reduced vapor pressure at a reduced temperature of 0.7. (Frequently the boiling point is near this temperature.) That means, we can apply the definition of the acentric factor to obtain a value of the vapor pressure relative to the critical point.