The Chemical Contribution to the Fugacity Coefficient and Compressibility Factor

The solution to phase equilibrium problems can be achieved in the manner of Chapter 15 (Eqn 15.20), where Eqns. 19.1 and 19.2 describe the enhanced equation of state. Eqns. 19.75–19.77 completely characterize the temperature, density, and composition dependence of the chemical contribution to Helmholtz energy. The Z^chem contribution is implied, but requires differentiation as in RT·Z^chem = –V∂(A – A^ig)/∂V. Similarly, the fugacity coefficient is implicitly determined through differentiation. Nevertheless, the differentiation can be complicated relative to the fugacity coefficient of the van der Waals model. The summation of Eqn. 19.77 means that terms like ∂X_i/∂n_j contribute and Eqn. 19.75 implies a nonlinear system of equations that must be solved to determine these contributions. For example, consider a mixture of three alcohols, with  and N_d,_i=1 for all i. Eqn. 19.75 implies that

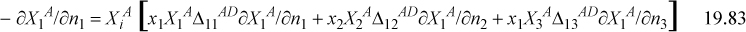
The only way to fully determine all ∂X_i/∂n_j is to apply Eqn. 19.75 eight more times to obtain nine equations for the nine unknown values implied by ∂X_i/∂n_j. Once again, chemical theory seems to become impractical.

Fortunately, this particular nonlinear system of equations possesses subtle but advantageous properties. Briefly, there are many symmetries in the calculus that lead to surprising simplifications when cleverly manipulated. Michelsen and Hendriks showed that A^chem can be rewritten as the stationary point of a generalized function Q.²⁰ The term “stationary point” refers to a condition where , for all i and B. At this time, there does not appear to be any underlying thermodynamic significance to the function Q or its stationary point. We apply it here merely as a mathematical device. The beauty of the generalized function is that derivatives with respect to  can be separated from derivatives with respect to V or n_j. By chain rule, and using  at the stationary point,

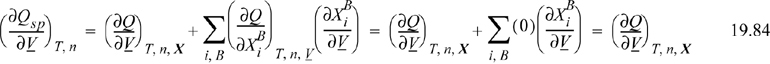
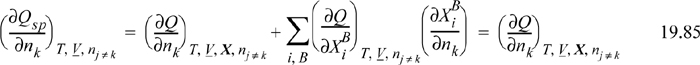
The generalized function, Q, can be inferred by adding and subtracting the defined term

from A^chem. The term h can then be rearranged through Eqn. 19.75 to obtain a function that is quadratic in acceptor/donor contributions by explicitly recognizing A/D contributions in place of the generic B. The algebra proceeds as,

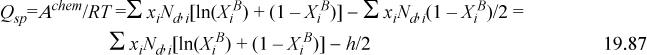
Expanding h in terms of  and  explicitly, and substituting for  and ,

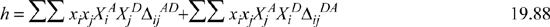
Now we recognize the generalized function with removal of the stationary point constraint.

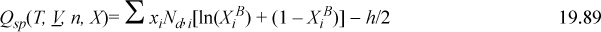
Note that the summation over  goes to zero when differentiated at the stationary point, so the term involving –h/2 is the only one that matters. Then we can take advantage of Eqns. 19.84 and 19.85 to obtain,

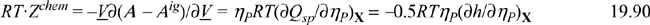
Differentiating Eqn. 19.88,

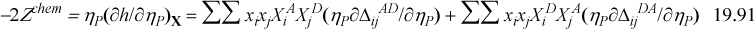
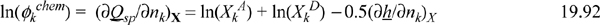
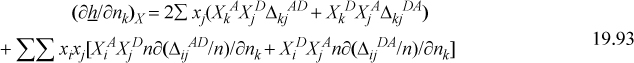
The derivative of Δ_ij^AD is straightforward, similar to Eqn. 19.54. Once again, the chemical contribution appears at first to be hopelessly complicated, but clever insights reduce the computational complexity to a level comparable with the Peng-Robinson model.

The computational complexity of Eqns. 19.75–19.77 can be further reduced in the special case where , which we refer to as the square root combining rule (SRCR). In general, Eqns. 19.75–19.77 require an iterative solution, as illustrated in Example 19.7. An initial guess for the iterations is

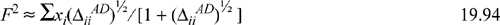
where  for all i,B. Note: . This simplification is accurate for alcohols and hydrocarbons, but not for alcohols and amines.²¹

This concludes our analysis of chemical contributions to phase equilibrium. Eqns. 19.75–19.77 and 19.91–19.93 permit solution of Eqns. 19.1 and 19.2 for mixtures as well as pure fluids and computation of the fugacity coefficients to perform any phase equilibrium determination. Wertheim’s theory of solution thermodynamics is more challenging than that of van der Waals or local compositions, but it replaces the empirical conjectures of those models with rigorous analysis that has been verified with molecular simulations. The perspective offered by Wertheim’s theory suggests further application of the basic equations to describe nonspherical molecules. This extension provides a self-consistent and rigorous description of the thermodynamics of all sizes of molecules, as discussed in the following section.