Always remember that ![]() depends on the standard state, which changes with temperature. Comparing Examples 17.2 and 17.3,
depends on the standard state, which changes with temperature. Comparing Examples 17.2 and 17.3, ![]() at 298 K (Ka = 1E-14), but decreases to
at 298 K (Ka = 1E-14), but decreases to ![]() at 900 K (Ka = 0.242). In order to calculate
at 900 K (Ka = 0.242). In order to calculate ![]() , it may seem that we need to know ΔGfo for each compound at all temperatures. Fortunately this is not necessary because the
, it may seem that we need to know ΔGfo for each compound at all temperatures. Fortunately this is not necessary because the ![]() can be determined from the Gibbs energy for the reaction at a certain reference temperature (usually 298.15 K) together with the enthalpy for the reaction and the heat capacities of the species.
can be determined from the Gibbs energy for the reaction at a certain reference temperature (usually 298.15 K) together with the enthalpy for the reaction and the heat capacities of the species.
Suppose we have a table of standard energies of formation at 298.15 K but we would like the value for ![]() at some other temperature. We can account for temperature effects by applying classical thermodynamics to the change in Gibbs energy with respect to temperature using the Gibbs-Helmholtz relation,
at some other temperature. We can account for temperature effects by applying classical thermodynamics to the change in Gibbs energy with respect to temperature using the Gibbs-Helmholtz relation,
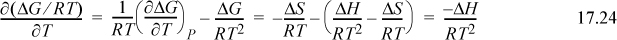
Jacobus Henricus van’t Hoff (1852–1911) was awarded the Nobel Prize in chemistry in 1901.
which results in the van’t Hoff equation:

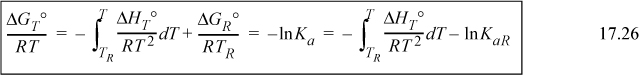
For accurate calculations, we must recognize that the heat of reaction depends on temperature. We have developed the standard heat of reaction in Section 3.6 and discussed the temperature dependence there. We show later that an assumption of a temperature-independent heat of reaction results in a short-cut approximation that is often close to the full calculation. We first show the full calculation. Substituting into the van’t Hoff equation (Eqn. 17.26) and integrating again,
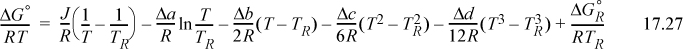
where we previously described finding J in Eqn. 3.46 on page 113. If desired, all values at TR can be lumped together in a constant, I.
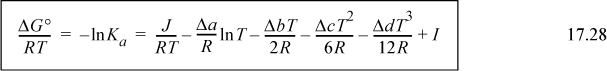
The constant I may be evaluated from a knowledge of ΔGo298 by plugging in T = 298.15 on the right-hand side as illustrated below.
Example 17.4. Equilibrium constant as a function of temperature
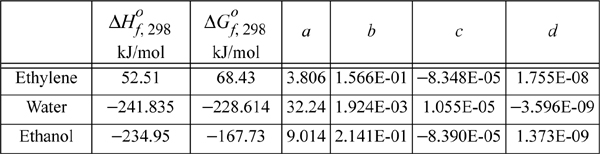
The heat capacities of ethanol, ethylene, and water can be expressed as CP = a + bT + cT2 + dT3 where values for a, b, c, and d are given below along with standard energies of formation. Calculate the equilibrium constant ![]() for the vapor phase hydration of ethylene at 145°C and 320°C.
for the vapor phase hydration of ethylene at 145°C and 320°C.
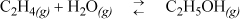
Solution
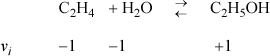
![]() The workbook Kcalc.xlsx or MATLAB Kcalc.m are helpful in doing these calculations.
The workbook Kcalc.xlsx or MATLAB Kcalc.m are helpful in doing these calculations.
Taking 298.15 K as the reference temperature,
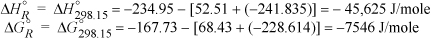
The variable J may be found with Eqn. 3.46 on page 113 at 298.15 K.
ΔH298.15o = –45,625 = J + ΔaT + (Δb/2)·T2 + (Δc/3)·T3 + (Δd/4)T4 = J + (9.014 – 3.806 – 32.24) T + [(0.2141 – 0.1566 – 0.0019)/2] T2 + [(–8.39 + 8.348 – 1.055)(1E-5)/3] T3 + [(1.373 –17.55 + 3.596)(1E-9)/4] T4
= J – 27.032 T + 0.02779 T2 – (3.657E-6)T3 – (3.145E-9)T4
Plugging in T = 298.15 K, and solving for J, J = –39.914 kJ/mole. Using this result in Eqn. 17.28 at 298.15 K will yield the variable I.
ΔGTo/RT = –39,914/(8.314·T) + 27.032/8.314 ln T – [(5.558E-2)/(2·8.314)] T +[(1.097E-5)/(6·8.314)]T2 + [(1.258E-8)/(12·8.314)]T3 + I
Plugging in ΔGRo at 298.15K, ΔGTo/RT = –7546/8.314/298.15 = 3.0442. Plugging in for T on the right-hand side results in I = –4.494.
The resultant formula to calculate ![]() at any temperature is
at any temperature is
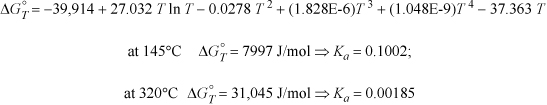
Leave a Reply