Supplement 3: Standard States

An important principle of the following discussion is that the chemical potential should be a property of the state of the system. All models should result in an identical value for the chemical potential at the same state. The standard state provides a convenient reference condition, but is slightly different from a reference state because it is at the same temperature as the system.³⁷

The typical convention for nonelectrolytes uses mole fractions and the Lewis-Randall standard state :

An alternative convention is related to the Henry’s law standard state  and the activity coefficient is known as the rational activity coefficient.³⁸

The activity coefficients on the two scales are related.

Inserting the activity coefficient relation into Eqn. 18.158 results in

Consider Eqn. 18.158. Inserting Eqn. 18.147 to replace the mole fraction,

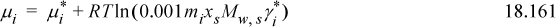
Because molality is not dimensionless, but activity is dimensionless, we must introduce some manipulations. We wish to introduce a molal activity coefficient, , to use with molal concentrations. The convention is to set the standard state as a hypothetical ideal solution, , at unit molality, m_o = 1 mol/(kg solvent). Introducing the standard state concentration (twice):

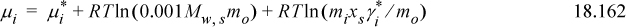
The unit value of m_o is traditionally omitted and thus “transparent.” We define the molal activity coefficient:

Note that Eqn. 18.147 can be reinserted into Eqn. 18.163 to eliminate x_s, if desired. Inserting Eqn. 18.163 into Eqn. 18.162,

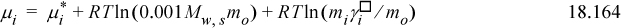
We can see that the standard state reference potential must be given by the first two terms on the right-hand side of the equation:

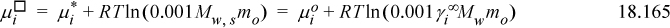
Substituting Eqn. 18.165 into Eqn. 18.164 results in the molal standard state and molal activity coefficient:

The activities corresponding to the standard states are thus

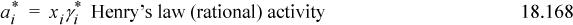
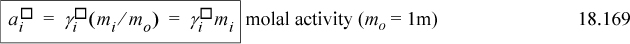
where the activities from the different scales are not equal at a given concentration because of the difference in standard states. Combining Eqns. 18.162 and 18.147,

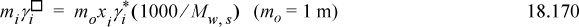
Finally, we note that the value of m_o is dropped from all the final expressions in application, based on the assertion that its value is 1 molal by the definition of the standard state. This is the basis for the equations presented in Sections 18.4 and 18.13.