Summary

A simple way of remembering the qualitative conclusions of this analysis can be derived by considering the behavior of the fugacity coefficient. One can easily demonstrate that the fugacity coefficient of the monomeric species is insensitive to the extent of association if it is expressed on the basis of the true number of moles in the associated mixture. But all of our phase equilibrium algorithms are based on the fugacity divided by the apparent mole fraction; for example, the flash algorithm is the same for any equation of state. The relation between the two fugacity coefficients is given by

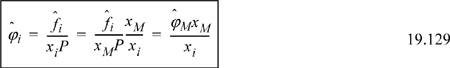
This means that we must simply multiply the fugacity coefficient from the usual equation of state expression by the ratio of true to apparent mole fraction. Since this ratio is always less than one, we see that the effect of association is to suppress the effective fugacity of the associating species.

For mixtures, elevation of the monomer mole fraction by breaking the association network accounts for VLE quite accurately. Fig. 19.12 illustrates the benefit of a chemical physical model relative to a purely physical equation like the Peng-Robinson equation. The figure depicting the methanol + cyclohexane system shows the improved accuracy in representing simultaneous LLE and VLE when hydrogen bonding is recognized. Notice the change in the skewness of the curves when hydrogen bonding is applied. The hydrogen bonding model is accomplishing this change in skewness as a clear and understandable explanation of the physics. By contrast, the van Laar model in Chapter 11 altered the skewness by adjusting constants that ignore the physics. We would expect that the stronger physical basis would provide greater capability for extrapolations to multicomponent mixtures. Unfortunately, remarkably few multicomponent studies have been performed to date. Hence, there is no single recommended method for treating nonideal multicomponent solutions at this time.

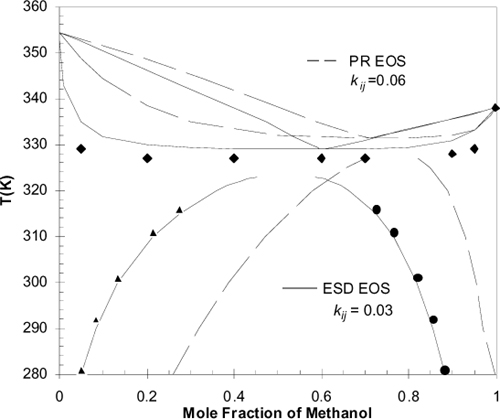
Figure 19.12. T-x-y diagram for the system methanol + cyclohexane. Data from Soerensen, J. M.; Arlt, W. Liquid-Liquid Equilibrium Data Collection; DECHEMA: Frankfurt/Main, 1979 Vol. V, Part 1.

From a theoretical perspective, however, we may still feel uncomfortable with having made several sweeping assumptions with little justification besides their making the equations easier to solve. This may not seem like much of an improvement over local composition theory. On the other hand, the assumptions could be reasonably accurate; they simply need to be tested. As in the case of local composition theory, molecular simulations provide an effective method of testing the assumptions implicit in the development of a theory. Fig. 19.13 shows a comparison to molecular simulation results and to Wertheim’s theory.³² It can be seen that the above assumptions lead to reasonably accurate agreement with the molecular simulations and therefore they represent at least a self-consistent theory of molecular interactions.

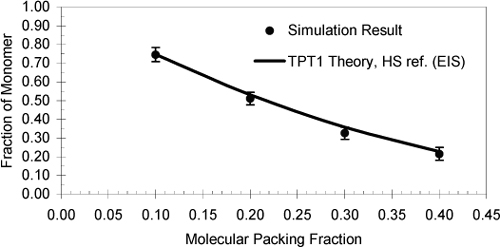
Figure 19.13. DMD-B simulation of hard dumbbell methanol with reduced bond length l/σ = 0.4, at T = 300 K and N_Aε_HB/R = 2013 K. TPT1 theory is an adaptation of Wertheim’s theory.

This is not to say that chemical theory completely solves all problems. Local composition effects are real and should be incorporated into the mixing rules. Evidence supporting this step can be found in the anomalous behavior of the methane + hexane system. If such local composition effects are so prominent for nonassociating solutions, they should be accounted for at all times. As an example of other problems, the association network of water seems to be different enough from that of alcohols that a more sophisticated model will be necessary to represent difficult solutions like hydrocarbons + water to the high degree of accuracy (ppm) required by organizations like the Environmental Protection Agency. Furthermore, the solvation between different species can be extremely complicated and require substantially more investigation to develop reliable engineering models. Finally, it is well known that “nonadditive” effects play a significant role in aqueous and alcoholic solutions.³³ That is, the energy of network formation changes in a way that cannot be understood based only on a simple potential model for a single water molecule. These peculiarities may seem esoteric, but they are key obstacles which prevent us from revealing many of the mysteries of biomolecular solutions. Other areas of application such as polymer solutions involving association, as in nylon, can also be imagined. These are the areas which remain to be explored. The methods for engaging in this exploration predominantly involve mathematically formalizing our treatment of the radial distribution function through applications of statistical mechanics. At this point, we leave this engagement to the “satisfaction and good fortune” of the reader.