Summary

This chapter began with a review of acid-base behavior to stress the importance of pH on equilibrium. Compounds are in the acid form below the pK_a,A and in the base form above. Techniques including Sillèn’s graphical method were provided to determine solution pH values and species distributions at various concentrations. We explained the origin of charges on biological molecules and why the charges change with pH, as well as the concept of zwitterions. Applications such as solubility, osmotic coefficients, and isoelectric point were developed.

Concepts of redox reactions were developed, relating the voltage to the Gibbs energy of reaction. Procedures were given to determine oxidation states, degree of reduction for molecules, and voltages in cells. The concept of oxidation and reduction in biological systems was introduced in the context of a biological fuel cell.

Binding polynomials were introduced as a method of representing simultaneous equilibria of families of pseudoisomers. The concepts of transformed Gibbs energies were introduced for biological systems buffered in pH or pMg.

Then solution nonidealities were introduced using the extended Debye-Hückel model. We finished the chapter by providing an example calculation of ATP distribution in nonideal solutions, and an example that couples phase equilibria with electrolyte equilibria. The later example demonstrates that for dilute solutions the graphical technique and simple arguments comparing the pH with the pK_a,A values provides rapid estimates that are valuable for converging to more precise values. Because pH and species concentrations vary over many orders of magnitude, the approximate methods are important to use first, and in many cases they are adequate for approximate engineering work. Ultimately, activity coefficient modeling is important for accurate calculations. The chapter concludes with some supplemental sections that are extremely valuable for conversions of the units used in the literature.

Important Equations

The most important equations of this chapter are the material balance, reaction equilibria, and electroneutrality relations. Unfortunately, these are different for every electrolyte system, so there is not much point in listing them the way we usually do in the chapter summary. A key step in using Sillèn’s method is to use the acid form of dissociations for weak electrolytes,

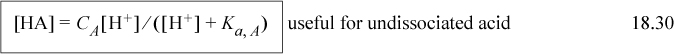
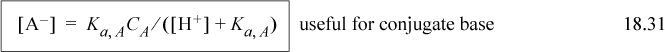
A new equation is the electroneutrality constraint. It is not a surprising equation, but it can cause difficulty because some species may be present in very small quantities that make very big differences–pH, for instance. Solving for these small quantities often requires rearranging the equations into a proton condition to avoid the precision problems that come with adding small numbers to large numbers.

In Section 18.11, the Nernst equation is important to relate voltage to standard potentials and actual concentrations, and the number of electrons transferred:

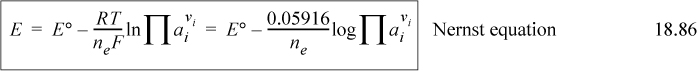
In Section 18.12 the Gibbs energy was transformed to use apparent concentrations. All the pH, pMg, and solution nonidealities were transferred to the Gibbs energies of reaction and the equilibrium constants:

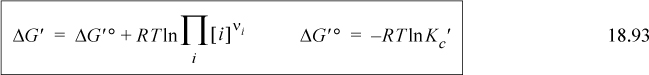
Besides the primary equations, the extended Debye-Hückel equation (Eqn. 18.107) is introduced in this chapter to account for nonideal behavior of ionic species. It is best limited to concentrations of 0.1 molal or less, but it conveys the concept that electrolyte solutions may deviate from ideality just as nonelectrolytes do. Going beyond Eqn. 18.107 would generally involve developing expertise beyond the introductory level.

Although the notation and reference states are obscure and frustrating, the implications are impressive. Salting in and salting out, protonation versus pH, osmosis, buffering, and leveling are just a few examples of implications that play significant roles in commonly encountered chemical systems, especially biological systems and corrosive environments. All the new jargon may seem overwhelming at first, but it can be assimilated if you only remember the three P’s: practice, practice, practice.