Summary

We have greatly enlarged the scope of our coverage of engineering thermodynamics with very little extension of the conceptual machinery. All we really did conceptually was recall that the Gibbs energy should be minimized. The provision that atoms can be moved from one chemical species to another with commensurate changes in energy and entropy simply means that reference states must be assigned to elemental standard states instead of standard states based on pure components, such that the free energies of all the components can be compared. In this sense we begin to comprehend in a new light the broad range of applications mentioned in Einstein’s quote at the end of Chapter 1. Instead of conceptual challenges, reaction equilibria focus primarily on the computational aspects of setting up and solving the problems. Notably, equation solvers can provide multidimensional capability. These are tools that can be adapted to many problems, even those beyond the scope of thermodynamics. You should familiarize yourself with such tools and build the expertise that will permit you to enhance your productivity.

Important Equations

The shortcut van’t Hoff equation provides a rapid method for screening the effect of temperature on the equilibrium constant. For best results, the temperature range should be limited as suggested in Section 17.8.

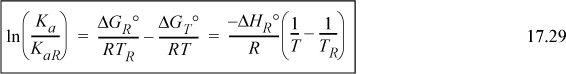
When combined with the equilibrium constraint Eqn. 17.15, reaction conversions can be estimated for many common scenarios.

The most common scenario is for ideal gases, because most industrial reactions are conducted at high temperature (to accelerate rates) and low pressure (to minimize cost).

For liquid phase components, we showed that the activity should be written as a_i = x_iγ_i. For solid species, we showed that the activity is unity when the solid is pure. The relevant Gibbs energy of formation must be used when liquids or solids appear in the equilibrium constant expression.

For simultaneous reaction and phase equilibria, we showed that the reaction could be treated in any one of the phases. Since the phase equilibrium constraint asserts equality of fugacity between phases, conceiving of the reaction in any particular phase is inconsequential, providing that the activities and Gibbs energies of formation use the same standard state.

Test Yourself

1. Reproduce the values given for the Gibbs energy of formation at 900 K for the component in Example 17.3. What values are given by the shortcut van’t Hoff equation?

2. Explain why a plot of lnK versus 1/T exhibits slight curvature.

3. When T is raised, the equilibrium constant is found to increase. Is the reaction endothermic or exothermic?

4. Explain why formation of a pure solid product does not inhibit a gas-solid reaction from going forward.

5. A reaction occurs with all components present in liquid and gas phases. Compositions in both phases are measured and the activities are calculated. The equilibrium constant value calculated using vapor phase activities is different from the equilibrium constant calculated using liquid phase activities. Is something wrong?

6. Describe the behavior of the reaction rate as equilibrium is approached. Explain why most industrial reactors are not run near equilibrium. Explain why calculation of an equilibrium constant is a good idea whenever designing a reactor.