Summary

The essence of the equation of state approach to mixtures is that the equation of state for mixtures is the same as the equation of state for pure fluids. The expressions for Z, A, and U are exactly the same. The only difference is that the parameters (e.g., a and b of the Peng-Robinson equation) are dependent on the composition. That should come as no large surprise when you consider that these parameters must transform from pure component to pure component in some continuous fashion as the composition changes. What may be surprising is the wealth of behaviors that can be inferred from some fairly simple rules for modeling this transformation. Everything from azeotropes to retrograde condensation, and even liquid-liquid separation can be represented with qualitative accuracy based on this simple extension of the equation of state.

So, are we done with phase behavior modeling? Unfortunately, the keyword in the preceding paragraph is “qualitative.” Equations of state are sufficiently accurate for most applications involving hydrocarbons, gases, and to some extent, ethers, esters, and ketones. For many oil and gas wells, it may suffice to treat the hydrocarbon-rich phases in this way and treat water separately. But any applications involving strongly hydrogen-bonding species tend to require greater accuracy than currently attainable from equations like the Peng-Robinson EOS. For example, if methanol is used as a hydrate inhibitor in a gas well, its partitioning may require a more sophisticated treatment. One idea is to adapt multiparameter activity models like the UNIQUAC model as the basis for mixing rules. This is the approach of the Wong-Sandler model.³ Another approach is to analyze hydrogen bonding as simultaneous reaction and phase equilibria, as discussed in Chapter 19.

Important Equations

Once again the mixing rules play an important role in defining the thermodynamics. Since the Peng-Robinson mixing rules have the same form as the van der Waals mixing rules, including a single binary interaction parameter, k_ij, the Peng-Robinson model cannot match the skewness of the Gibbs excess curve, only the magnitude. Outside the critical region, you might as well use an activity model. The advantage of the Peng-Robinson model is that it provides a holistic framework that applies seamlessly to vapor, liquid, and critical region. Noting how activity models artificially designate different methods for different phases, it is gratifying to see that such conceptual simplicity is feasible. The key equation for establishing this feasibility is deriving the fugacity coefficient for a pressure-explicit equation of state:

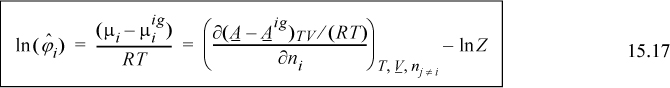
Given this equation, it is straightforward to derive fugacity coefficients, and K-ratios, for any equation of state or mixing rule. Two related equations that often appear are Eqns. 15.23 and 15.26.

Look for ways to rearrange the equations before differentiating such that these terms appear and then differentiation becomes much simpler, often reducing to simple substitution. Finally, the EOS method melds with every other phase equilibrium computational procedure when the expression is derived for the partition coefficient, as given by a slight variation on Eqn. 15.20.

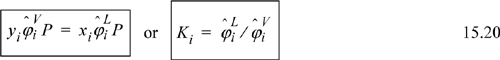
Here we have generalized Eqn. 15.20 slightly by recognizing that the upper phase could be vapor or it could be the upper phase of LLE. The beauty of the EOS perspective is that the fluid phase model is the same for liquid or vapor; only the proper root must be selected.