Summary

This has been a somewhat theoretical chapter. We have gone through iterations of observation, prediction, testing, and evaluation with several theories (e.g., van Laar, Scatchard-Hildebrand, Flory-Huggins, SSCED, and MOSCED). With each iteration, we have achieved increasing precision and insight. Sulfuric acid and water may react very favorably toward each other (G^E << 0), while 2-propanol and water have enhanced escaping tendencies because the energy required for forcing them to mix is counteracting the entropic driving force (G^E > 0). These facts are due in large part to the interaction energies characterized by molecular quantities like the solubility parameter, acidity, and basicity. We showed that two major effects influence the mixing: energy density and complexation. This molecular perspective provides clarification of the familiar guideline that “like dissolves like.” With this perspective, we begin to acquire the capability to intuitively reason about chemical formulations. We illustrated the value of this reasoning with several practical examples. You should be able to distinguish favorable molecular interactions from unfavorable.

Carrying forward the molecular perspective, we can characterize these tendencies in terms of the cross-interaction energy (a₁₂). If the cross-interaction energy is weaker than the geometric mean (k₁₂ > 0), then each component prefers its own company. If the cross-interaction energy is stronger than the geometric mean (i.e., k₁₂ < 0), then the components are strongly attracted, releasing energy as they fall into the well of their mutual attraction. The energy to break the favorable interactions must be added to separate such a mixture and this may show up as a maximum boiling azeotrope. Conversely, mixtures with k₁₂ > 0 tend to exhibit minimum boiling azeotropes, or VLLE if γ_i > 10.

Molecular insight can help a lot when conceiving of formulations, but these conceptions must ultimately be tested and validated experimentally.

Important Equations

This chapter has built the connection between the molecular perspective offered by the van der Waals model and semi-empirical estimates of activity coefficients for binary and multicomponent mixtures. The key equations in this extension are

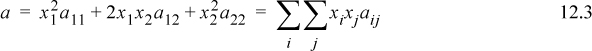
where k₁₂ is an adjustable parameter called the binary interaction parameter.

This extension results in several closely related activity models of varying complexity. The choice of the “best” model depends on the application and the individual’s comfort level with a particular degree of complexity. As a summary, the SSCED model provides a reasonable compromise.

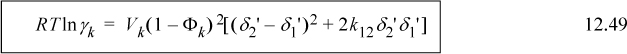
With this equation, the important roles of energy density (δ² ≡ a/V²), molecular size (V_k), and hydrogen bonding are all evident. Understanding these roles enables you to go beyond fitting data and make predictions about the behavior to be expected when various chemicals are combined. With practice, these predictions evolve to provide intuitive insight into formulations that achieve specific engineering objectives.