Shortly after Wertheim’s work appeared, Chapman et al. formulated an equation of state that incorporated the bonding contribution and complexation as well as the disperse repulsive and attractive terms. Their perspective was to treat any solution in the conventional way as a fluid of independent spheres, then to add the bonding contribution required to assemble the spheres into chains. Then the equation of state becomes

Adding and subtracting (1 – m) to isolate the ideal gas limit,
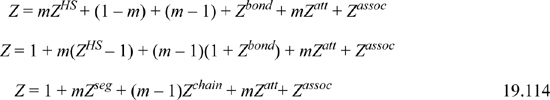
Recognizing the significance of Wertheim’s statistical mechanical theory for associating (and solvating) systems, Chapman et al. named their model SAFT. In principle, any equation of state can be applied for the dispersion interactions, but Chapman et al. adopted the Carnahan-Starling model for the hard-sphere systems, including the Mansoori-Carnahan-Starling-Leland (MCSL) model for hard-sphere mixtures.23 That choice has remained consistent in most variations of the SAFT model, but several alternatives have been adopted to describe the attractive dispersion interactions, Zatt. The original version suggested using second order perturbation contributions of the Lennard-Jones fluid for Zatt.24 Huang and Radosz adopted a 20-parameter equation of state for argon (HR-SAFT).25 More recently, Gross and Sadowski took a slightly different approach.26 They treated the hard-sphere and chain contributions in the usual manner of SAFT, but treated Zatt by a second order perturbation theory that takes the tangent-sphere-chain as the reference fluid, instead of the tangent spheres themselves. They refer to their method as Perturbed Chain SAFT (PC-SAFT). In the conventional SAFT approach, Zatt/m would be a universal curve, but PC-SAFT shows a mild variation in this quantity with chain length. We focus our discussion on PC-SAFT for the most part.
Chapman et al. (1990)a suggested that second order perturbation theory could be applied for the segment term of the SAFT model, with the hard-sphere contribution described by the Carnahan-Starling (CS) equation and the Aatt given by:
Aatt/RT = A1βε + A2(βε)2
A1 = –11.61ηP – 8.28ηP2 – 5.24ηP3 + 34.21ηP4
A2 = –25.76ηP + 181.87ηP2 – 547.17ηP3 + 529.00ηP4
Express this model as an equation of state for alcohols, including Zchain; that is Z = Z(m,ηP,βε).
Solution
The CS equation is given by Zhs–1 = 4ηP(1 – ηP/2)/(1 – ηP)3. This corresponds to g(σ) = (1 – ηP/2)/(1 – ηP)3 and, by Eqn. 19.44, Δ = ρ(1 – ηP/2)KAD(exp(βεijAD) – 1)/(1 – ηP)3. Then, ∂lnΔ/∂lnηP = ηP{Δ/η – Δ/(2 – ηP) + 3Δ/(1 – ηP)} = Δ{1 + (5ηP – 2ηP2)/[(2 – ηP)(1 – ηP)]}.
Substituting,
Zchain = Zbond + (m – 1) = –(m – 1)(Zbond – 1) = –(m – 1)(5ηP – 2ηP2)/[(2 – ηP)(1 –ηP)]
Zchem = –0.5h∂lnΔ/∂lnηP = –(1 –XA) ∂lnΔ/∂lnηP = –(1 – XA){1 + (5ηP – 2ηP2)/[(a – ηP)(1 – ηP)]}; and Zseg = Zhs – 1 + Z1βε + Z2(βε)2, where Z1 = –11.61ηP – 16.56ηP2 – 15.72ηP3 + 136.84ηP4 and Z2 = –25.76 ηP + 363.74ηP2 – 1641.51ηP3 + 2116.00ηP4.
Putting it all together, Z(m,ηP,Tr)= 1 + m[4ηP(1 – ηP/2)/(1– ηP)3 + Z1βε + Z2(βε)2] – (m – 1)(5ηP – 2 ηP2)/[(2 – ηP)(1 – ηP)] – (1 – XA){1+(5ηP – 2ηP2)/[(2 – ηP)(1 –ηP)]}.
where XA = [–1 + (1 + 4Δ)1/2]/(2Δ), Δ = ηP(1 – ηP/2)(KAD/b)(exp(Hβε) – 1)/(1 – ηP)3, H = εijAD/ε. Since all the terms can be computed based on m,ηP, βε, the equation of state is complete.
a. Chapman, W.G., Gubbins, K.E., Jackson, G., Radosz, M. 1990. Ind. Eng. Chem. Res. 29:1709.
The tangent-sphere-chain that lays the foundation of all SAFT models is well defined and relatively simple to treat by molecular simulation. This makes it possible to evaluate the accuracy of Wertheim’s theory for the hard chain reference system. With only slightly more effort we can also evaluate the accuracy for a reference fluid of fused sphere chains with 110° bond angles, as in n-alkane chains. As shown in Fig. 19.11, the comparison is quite favorable in both cases, showing that Wertheim’s theory and the related SAFT models have a solid theoretical foundation that is validated by molecular simulation.
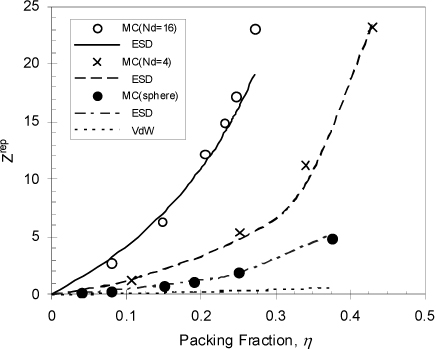
Figure 19.11. Comparison of molecular simulations, the van der Waals equation, and the ESD equation of state for Zrep. Nd is the number of spheres in a chain.
The PC-SAFT model has the same form as Example 15.8 except for Zattseg.
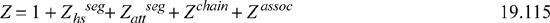
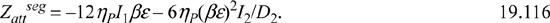

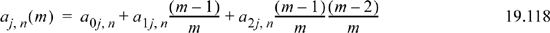
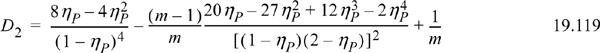
Eqns. 19.117 and 19.118 include 42 coefficients listed in the original reference.
You might wonder whether there is a simpler form of the SAFT model that is more sophisticated than the van der Waals model, but not as complicated as the PC-SAFT model. Such a model would be convenient for illustrating the key advantages of an association model without losing the simplicity of a cubic model like the PR model. One alternative is simply to add the association contribution of Example 15.8 to the PR model. This is the basis of the CPA model of Kontogeorgis et al.27 This is a feasible model and it has been applied in many practical settings, but it is not entirely faithful to the Wertheim perspective in that it uses g(σ) from one model and Zhs from another, while ignoring Zchain completely. Another alternative is to reconsider the ESD model in light of the SAFT analysis. Then we can rewrite the ESD model as a “simplified SAFT” model:28
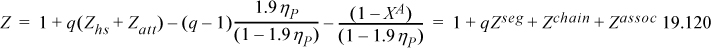
In this form, we recognize that g(σ)=1/(1–1.9ηP) provides consistency as a SAFT model. Then,
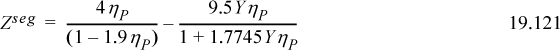


Leave a Reply