Speciation and the Dissociation Constant

The term speciation refers to a cataloging of the species that exist in solution. The species are characterized by writing dissociation reactions that identify the species and material balance constraints that exist in solution. To introduce the concepts of speciation, consider the dissociation of water:

Thus, in pure water, the species in solution are H₂O, H⁺, and OH^–. From introductory chemistry courses, we are familiar with this reaction and the equilibrium constant at 25°C:

Another important concept in speciation is that the solution must satisfy a charge balance, and the net charge in solution must be zero. While the charge balance is trivial for this example, it becomes important in setting up the mathematical solutions to the material balances.

Eqn. 18.5 contains some implicit assumptions that are rarely explained in introductory chemistry books. From our discussion in Chapter 17, we know that a rigorous calculation should use activities for a chemical reaction:

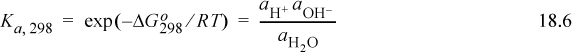
Comparing the last two equations, we recognize that Eqn. 18.6 can be simplified to Eqn. 18.5 if the activities of ions are replaced with concentrations, and if the activity of undissociated water is unity. Certainly the approximations of Eqn. 18.5 are valid under common conditions or the introductory textbooks would have been in error. But what is meant by the activity of ions, and why does the activity of water not appear in Eqn. 18.5? To understand the simplifications, we must understand the various concentration conventions. The subtleties are important because the values of the equilibrium constants that characterize the reactions are coupled to the concentration and activity scales.

To partially clarify the relation between Eqns. 18.5 and 18.6, it is necessary to recall that activity is dimensionless but molarity has dimensions of mol/L. This issue is subtly handled by using molal concentrations and defining the standard state for electrolytes to be an ideal solution at m° = 1 molal. Therefore, Eqn. 18.6 can be successively converted using  where the m° states are equal to 1 molal, the molal activity coefficients are ignored, and the molar concentration is used as an approximation to the molality. Water disappears from the relation because the water standard state is taken as purity and a neutral solution is virtually pure water.⁴ Supporting discussion is provided in Sections 18.13–18.15 and summarized in Section 18.24.

Measuring Speciation

Quantitative speciation is important in development of a proper thermodynamic model. Various techniques are used, including absorption, NMR and Raman spectroscopies, conductance, emf, solubilities, and rates of reaction. Most techniques require estimation of the activity coefficients to extrapolate to infinite dilution where the K_a is calculated from ideal solution approximations. Because modeling extrapolation is always necessary to “measure” the constants, considerable scatter among literature values is common.