When a solid component is involved in a reaction, the fugacity ratio for activity in Eqn. 17.15 is typically expressed using activity coefficients. For a solid solution,
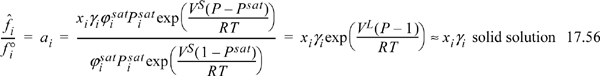
where P is expressed in bar, Psat represents the solid sublimation pressure, and the Poynting correction is often negligible. Commonly, multiple solids exist as physical mixtures of pure crystals as discussed in Section 14.10 on page 556. When the solids are immiscible, Eqn. 17.56 simplifies to
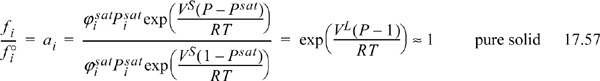
Similar to working with liquids, solid phase data are used for 
, not the ideal gas values. When these values are not available in the literature, it is common to express equilibrium in terms of temperature-dependent correlations for Ka as described in Section 17.18.
Consider the reaction:
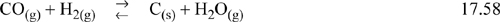
The carbon formed in this reaction comes out as coke, a solid which is virtually pure carbon and separate from the gas phase. What is the activity of this carbon? Since it is pure, aC = 1. Would its presence in excess ever tend to push the reaction in the reverse direction? Since the activity of solid carbon is always 1 it cannot influence the extent of this reaction. How can we express these observations quantitatively? Eqn. 17.15 becomes
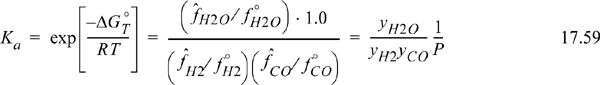
To compute ΔGoT as a function of temperature, we apply the usual van’t Hoff procedure. This means that CP,c can be treated just like CP of the gaseous species.
Example 17.11. Thermal decomposition of methane
A 2-liter constant-volume pressure vessel is evacuated and then filled with 0.10 moles of methane, after which the temperature of the vessel and its contents is raised to 1273 K. At this temperature the equilibrium pressure is measured to be 7.02 bar. Assuming that methane dissociates according to the reaction 
, compute Ka for this reaction at 1273 K from the experimental data.
Solution
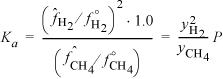
We can calculate the mole fractions of H2 and CH4 as follows. Since the temperature is high, the total number of moles finally in the vessel can be determined from the ideal gas law (assuming that the solid carbon has negligible volume): n = PV/RT = 0.702·2000/(8.314)(1273) = 0.1327. Now assume that ξ moles of CH4 reacted. Then we have the following total mass balance: nT = 0.10 + ξ. Therefore, ξ = 0.0327 and
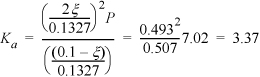
Note that the equilibrium constant indicates that significant decomposition will occur (the reaction is exergonic, Ka > 1) and that graphite forms. Such behavior is known as “coking” and is common during industrial catalysis. Industrial application of catalysis often includes consideration of “regeneration’” of the catalyst by burning off the coke and using the heat of combustion elsewhere in the chemical plant.
Leave a Reply