It is not difficult to imagine situations in which reactions take place in the presence of multiple phases. Absorption of CO2 into NaOH solution involves a reaction of the CO2 as it dissolves to form sodium bicarbonate and sodium carbonate. Hydrogen bonding in “pure” fluids implies reaction and phase equilibrium at saturation conditions. The production of methyl t-butyl ether (MTBE) as an oxygenated fuel additive is an interesting process in which catalyst is placed on the trays of a distillation column. As catalysts are developed which are active at progressively lower temperatures, multiphase reactions should become even more common. In low-temperature methanol synthesis (~240°C), it can be advantageous to add a liquid phase to absorb the heat of reaction, as described in the example below. Biological pathways are also in development for many products, which frequently involve multiple phases.
The thermodynamic analysis of this seemingly complex kind of process is actually very similar to the analysis of multireaction equilibria. The extent of formation of a second phase is analogous to a reaction coordinate. The easiest way to illustrate the formulation of the problem is to consider an example. Suppose the methanol synthesis reaction was carried out at 75 bars and 240°C such that the gas phase mole fractions were 0.25 CO, 0.25 MeOH, and 0.50 H2. Based on a stoichiometric feed composition, the conversion would then be 50%. Now suppose this gas phase was placed in contact with a liquid phase with a nonvolatile solvent. The K-ratios at these conditions are about 10 for CO and H2, and about 1.0 for MeOH. What would be the composition in the liquid phase and the extent of conversion if only liquid was removed? The composition of the liquid would be 0.025 CO and 0.25 MeOH. Therefore, the extent of conversion would be 0.25/0.275 = 91%. Thus, the addition of a liquid phase greatly enhances conversion of this process. The example below elaborates on these findings in a much more formal manner.
Example 17.15. The solvent methanol process
In a process being considered for methanol synthesis, a heavy liquid phase is added directly to the reactor to absorb the heat of reaction. The liquid is then circulated through an external heat exchanger. Usually, the catalyst is slurried in the liquid phase. An alternative to be considered is putting the catalyst in a fixed bed and adding just enough liquid so that a fairly small amount of vapor is left at the end of the reaction. Supposing naphthalene was used as the heavy liquid phase, use the Peng-Robinson equation to obtain approximate vapor-liquid K-value expressions of the form
for each component at a temperature of 200–250°C and pressures from 50–100 bar.a In the worksheet computations, you may assume the K-value of naphthalene to be negligible.
Solution
A worksheet used for this solution is available in the workbook Rxns.xlsx.
Computing the K-value would normally require calling the Peng-Robinson equation during every flash and reaction iteration. This approximate correlation enables you to use Excel to perform the calculations since it is independent of any external programming requirements. The correlation should be suitably accurate if you “guess” compositions for developing the correlation that are reasonably close to the compositions at the outlet of the reactor. We suggest a guess for feed composition of {0.02, 0.10, 0.02, 0.035, 0.005, 0.82} for {CO, H2, CO2, methanol, water, and naphthalene}.
As an example of a way to develop a synthetic data base, perform flash calculations at 75 bars and temperatures of {200, 210, 220, 230, 240, 250} and the suggested feed composition. Tabulate the K-values for each component and plot them logarithmically with reciprocal temperature on the abscissa. Select a set of points, then select “add trendline” from the Chart menu. Select the options for a logarithmic fit, and displaying the equation on the chart. The coefficients of the equation give the a and b for the local “shortcut” correlation. (This step simplifies the implementation in Excel, but would be unnecessary if you were writing a dedicated program with access to a Peng-Robinson subroutine.)
Designating the solvent as component 6, the vapor-liquid K-values can be estimated as follows.

Solve for the simultaneous reaction and phase equilibria at 240°C and P = 100 bars considering the following two reactions:
Add moles of the heavy liquid until 9 moles of liquid is obtained for every mole of vapor output. The gases are fed in proportions 2:7:1 CO:H2:CO2.
Applying the shortcut van’t Hoff equation (calculated at 503 K using lnKa and ΔH°R, all reacting species gases),
Stoichiometry

Imagine performing a flash at each new extent of conversion:
Writing objective functions:
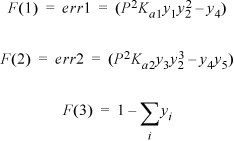
This worksheet is called SMPRXN. An example of the output from a feed of 2,7,1,0,0 mole each of CO, H2, CO2, CH3OH, H2O is shown in Fig. 17.7.
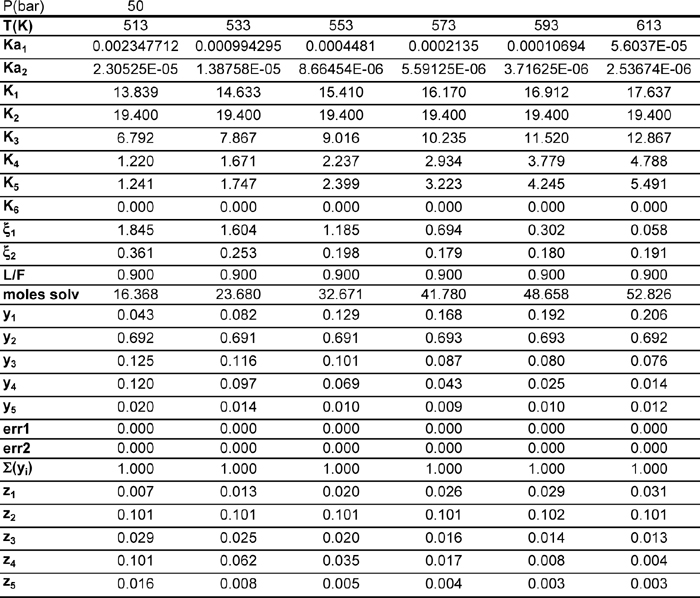
Figure 17.7. Worksheet SMPRXN from workbook Rxns.xlsx for Example 17.15 at several temperatures.
The method of solving this problem is extremely similar to the DUALRXN problem. The only significant addition is an extra constraint equation which specifies that the vapor mole fractions must sum to unity. Note that ξ1 is greater than unity. This is because we have 2 moles of CO in the feed, so 1.3 moles converted is about 65%.
a. Note: The symbols a and b are simply regression coefficients, not the equation of state parameters a and b.
Example 17.16. NO2 absorptiona
The strength of concentrated acid which can be produced is limited by the back pressure of NO2 over the acid leaving the absorbers. The overall reaction, obtained by adding reactions (a) and (b), is shown as (c). Here we assume that N2O4 is equivalent to 2NO2.
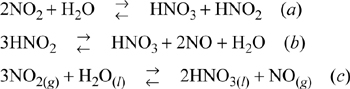
The gas entering the bottom plate of a nitric acid absorber contains 0.1 mole of NO per mole of mixture and 0.25 mole of NO2 per mole mixture. The entering gas also contains 0.3 bar partial pressure of oxygen, in addition to inert gas. The total pressure is 1 bar. The acid made by the absorption operation contains 50% by weight of HNO3, and the operation is isothermal at 86°F. Estimate the composition of the gas entering the second plate and the strength of the gas leaving the second plate.
Solution
(Basis: 1 mole gaseous feed)
Assume yw = yHNO3 = 0 and xNO2 = xNO = 0.
For liquid:
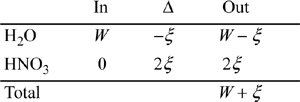
For vapor:
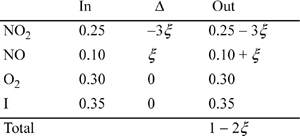
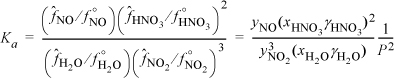
We can determine the mole fractions from the weight fractions:
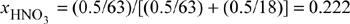
Noting from the CRC Handbookb the vapor pressure of HNO3 is 64.6 mmHg, we can estimate the activity coefficients of HNO3 and water from the x-y data in The Chemical Engineers’ Handbook.c
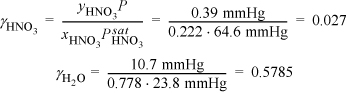
Gibbs energies of formation are available in Appendix E for all but nitrogen dioxide, and Reid et al.d give the standard Gibbs energy of formation as 52 kJ/mol and the standard heat of formation as 33.87 kJ/mol. Performing a shortcut calculation using Kcalc.xlsx, the equilibrium constant at 303.15 K is Ka = 0.0054.
At P = 1 bar:
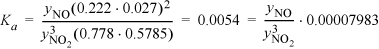
Substituting for the reaction coordinate:
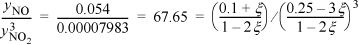
Solving the cubic equation, ξ = 0.0431.
xHNO3 = (2ξ/(W + ξ) = 2·0.0431/(W + 0.0431) = 0.222 tells us that
W = –0.0431 + 2·0.0431/0.222 = 0.345 moles
So the composition of gas entering the second stage is yNO = 0.157; yNO2 = 0.132; yO2 = 0.328; yI = 0.383. Computations for further stages would be similar.
a. S. Lee, Personal Communication, 1993.
b. Weast, R.C. 1979. CRC Handbook of Chemistry and Physics, 60th ed, Boca Raton, FL: CRC Press, p. D-224.
c. Perry, R.H., Chilton, C.H. 1986. The Chemical Engineers’ Handbook, 6th ed. New York, NY: McGraw-Hill, p. 3–70.
d. Reid, R.C., Prausnitz, J.M., Poling, B. 1987. The Properties of Gases & Liquids, 4th ed, New York, NY: McGraw-Hill.
Leave a Reply